HOW TO FIND RADIUS WHEN LENGTH OF TWO PARALLEL CHORDS ARE GIVEN

Here we are going to see some examples problems on finding radius when length of two parallel chords are given.

Example 1 :

AB and CD are two parallel chords of a circle which are on either sides of the centre. Such that AB = 10 cm and CD = 24 cm. Find the radius if the distance between AB and CD is 17 cm.

Solution :

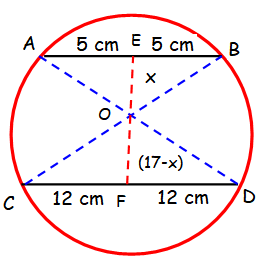
Consider the right triangles OEB and OFD,

OB = OD (radius of the given circle)

(1)  =  (2)  

x² + 5²  =  (17-x)² + 12²

x² + 5²  =  17² + x² - 2(17) x + 12²

x² + 25  =  289 + x² - 34x + 144

x² - x² + 34x + 25 - 144 - 289  =  0

34x - 408  =  0

34(x - 12)  =  0

x  =  12 cm

By applying the value of x in the 1^st equation, we get

OB²  =  12² + 5² 

OB²  =  144 + 25  =  169

OB  =  √169  =  13 cm

Example 2 :

In the figure given below, AB and CD are two parallel chords of a circle with centre O and radius 5 cm such that AB = 6 cm and CD = 8 cm. If OP ⊥ AB and CD = OQ determine the length of PQ.

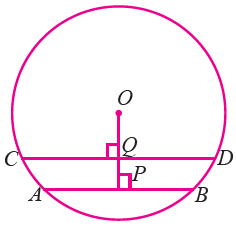
Solution :

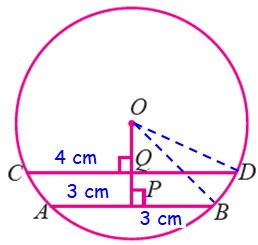
Here we have two right triangles,

Triangle OPB and triangle OQD.

OB =  OD  =  radius of the circle  =  5 cm

In Δ OPB,

PQ  =  OP - OQ

  =  4 - 3

  =  1 cm

Hence the length of PQ is 1 cm

Example 3 :

In the figure given below, AB and CD are two parallel chords of a circle with centre O and radius 5 cm. Such that AB = 8 cm and CD = 6 cm. If OP = AB and OQ ⊥  CD.determine the length PQ.

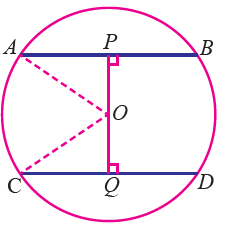
Solution : 

Consider the triangles APO and COQ

OA  =  OC  =  radius of the circle  =  5 cm

AP  =  PB  =  4 cm

CQ  =  QD  =  3 cm

PQ  =  PO + OQ

  =  3 + 4

  =  7 cm

Hence the length of PQ is 7 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.