HOW TO FIND MODULUS OF A COMPLEX NUMBER

Let z = a + ib be a complex number.

The modulus or absolute value of z denoted by | z | is defined by

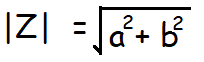
Modulus of complex number properties

Property 1 :

The modules of sum of two complex numbers is always less than or equal to the sum of their moduli.

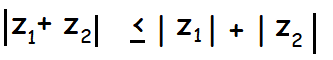
The above inequality can be immediately extended by induction to any finite number of complex numbers i.e., for any n complex numbers z₁, z₂, z₃, …, z_n

|z₁ + z₂ + z₃ + … + zn | ≤ | z₁ | + | z₂ | + … + | z_n |

Property 2 :

The modulus of the difference of two complex numbers is always greater than or equal to the difference of their moduli.

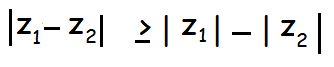
Property 3 :

The modulus of a product of two complex numbers is equal to the product of their moduli.

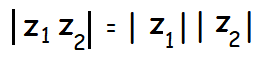
Property 4 :

The modulus of a quotient of two complex numbers is equal to the quotient of their moduli.

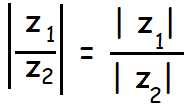
Let us look into some examples based on the above concept.

Example 1 :

Find the modulus of the following complex number

− 2 + 4i

Solution :

Let z  =  -2 + 4i

|z|  =  √(-2 + 4i)

|z|  =  √(-2)² + 4² 

  =  √4 + 16

  =  √20

By decomposing the number inside the radical, we get

  =  √(2 ⋅ 2 ⋅ 5)

  =  2√5

Example 2 :

Find the modulus of the following complex number

2 − 3i

Solution :

Let z  =  2 − 3i

|z|  =  √(2 - 3i)

|z|  =  √2² + (-3)² 

  =  √4 + 9

  =  √13

Example 3 :

Find the modulus of the following complex number

− 3 − 2i

Solution :

Let z  =  − 3 − 2i

|z|  =  √(− 3 − 2i)

|z|  =  √(-3)² + (-2)² 

  =  √9 + 4

  =  √13

Example 4 :

Find the modulus of the following complex number

4 + 3i

Solution :

Let z  =  4 + 3i

|z|  =  √(4 + 3i)

|z|  =  √4² + 3² 

  =  √16 + 9

  =  √25

By decomposing the number inside the radical, we get

  =  √(5 ⋅ 5)

=  √5

Let us look into the next example on "How to find modulus of a complex number".

Example 5 :

Find the modulus or absolute value of

[(1 + 3i) (1 - 2i)] / (3 + 4i)

Solution :

|[(1 + 3i) (1 - 2i)] / (3 + 4i) |  =  |(1 + 3i) (1 - 2i)| / |3 + 4i|

  =  |(1 + 3i)| |(1 - 2i)| / |3 + 4i|

  =  √(1² + 3²) √(1² + (-2)²)  / √3² + 4²

  = ( √(1 + 9) √(1 + 4))  / √(9 + 16)

  = ( √10 √5)  / √25

  =  √50 / √25  =  5√2/5  =  √2 

Related topics

• Properties of complex numbers
• Add and subtract complex numbers
• How to find the modulus and argument of a complex number
  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.