HOW TO FIND INTERQUARTILE RANGE FOR UNGROUPED DATA

Example 1 :

For the data set 7, 3, 4, 2, 5, 6, 7, 5, 5, 9, 3, 8, 3, 5, 6

(a)  Median  (b)  Lower quartile 

(c)  Upper quartile  (d)  Interquartile range

Solution :

7, 3, 4, 2, 5, 6, 7, 5, 5, 9, 3, 8, 3, 5, 6

Number of elements  =  15 (odd)

To find median, arrange the data set from least to greatest.

2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 7, 8, 9

Median  =  (n+1) /2 ^th element

=  (15+1) /2 ^th element

=  8^th element

(a)  Median (Q₂)  =  8^th element

 Median (Q₂)  =  5

(b)  2, 3, 3, 3, 4, 5, 5

Lower quartile (Q₁)  =  5

(c)  5, 6, 6, 7, 7, 8, 9

Upper quartile (Q₃)  =  7

(d)  Inter quartile range  =  Q₃ - Q₃

=  7 - 5

=  2

So, the  interquartile range is 2.

For the data set given below, find the following.

(a) median   (b) lower quartile

(c) upper quartile (d) interquartile range.

Example 2 :

6, 10, 7, 8, 13, 7, 10, 8, 1, 7, 5, 4, 9, 4, 2, 5, 9, 6, 3, 2

Solution :

1, 2, 2, 3, 4, 4, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9, 10, 10, 13

Number of data values  =  20 (even)

median  =  {(n/2)^th term + [(n/2) + 1]^th term}/2

=  (10^th term + 11^th term)/2

=  (6+7)/2

=  13/2

=  6.5

1, 2, 2, 3, 4, 4, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9, 10, 10, 13

(b)  Lower quartile (Q₁)  =  4

(c)  Upper quartile (Q₃)  =  9

(d)  Interquartile range  =  9-4  ==> 5

Example 3 :

6, 4, 7, 5, 3, 4, 2, 6, 5, 7, 5, 3, 8, 9, 3, 6, 5

Solution :

2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 8, 9

Number of data values  =  17 (odd)

median  =  (n + 1)/2^th term

= (17 + 1)/2^th term

= (18/2)^th term

= 9^th term

median = 5

2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 8, 9

(b)  Lower quartile (Q₁)  =  (3 + 4)/2 ==> 3.5

(c)  Upper quartile (Q₃)  =  (6 + 7)/2 ==> 6.5

(d)  Interquartile range  =  Q₃ - Q₁

= 6.5 - 3.5

= 3

Example 4 :

11, 6, 7, 8, 13, 10, 8, 7, 5, 2, 9, 4, 4, 5, 8, 2, 3, 6

Solution :

11, 6, 7, 8, 13, 10, 8, 7, 5, 2, 9, 4, 4, 5, 8, 2, 3, 6

Arranging from least to greatest,

2, 2, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 8, 9, 10, 11, 13

Number of data values  =  18 (even)

= {(n/2)^th term + [(n/2) + 1]^th term}/2

=  (9^th term + 10^th term)/2

= (6 + 7)/2

= 13/2

median = 6.5

2, 2, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 8, 9, 10, 11, 13

(b)  Lower quartile (Q₁)  =  (4 + 4)/2 ==> 4

(c)  Upper quartile (Q₃)  =  (8 + 9)/2 ==> 8.5

(d)  Interquartile range  =  Q₃ - Q₁

= 8.5 - 4

= 4.5

Example 5 :

for the data set given, find

Solution :

20, 21, 22, 22, 30, 30, 31, 34, 34, 35, 38, 40, 42, 43, 44, 46, 46, 49, 51, 51, 54, 55, 58

a) The minimum value = 20

b) The median :

Total number of terms = 23 (odd)

= (23 + 1)/2

= 24/2^th value

= 12^th value

= 40 is the median

c) The maximum value = 58

d) The upper quartile :

20, 21, 22, 22, 30, 30, 31, 34, 34, 35, 38, 40, 42, 43, 44, 46, 46, 49, 51, 51, 54, 55, 58

The upper quartile = 40

Median of upper part :

20, 21, 22, 22, 30, 30, 31, 34, 34, 35, 38

Q₁ = 30

e) Median of lower part :

42, 43, 44, 46, 46, 49, 51, 51, 54, 55, 58

Q₃ = 49

Lower quartile = 49

f) range = maximum value - minimum value

= 49 - 30

= 19

Example 6 :

Two classes have completed the same test. Box lots have been drawn to summaries and display the results. They have been on the same set of axes so that the results can be compared.

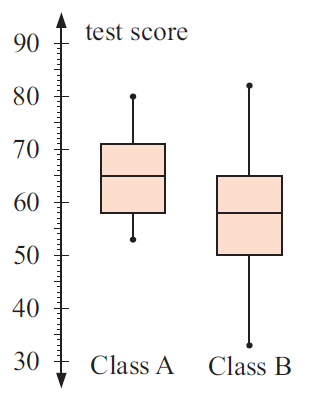
In which class was.

a) highest mark

b) the lowest mark.

c) the range of marks in class B

d) the interquartile range of class A.

Solution :

a)

Highest mark in class A = 80

class B = 83

b)

lowest mark in class A = 52

in class B = 33

c) Range in class B = 83 - 33

= 50

d)  interquartile range of class A = 

Q1 = 58 and Q3 = 71

= 71 - 58

= 13

Related Pages

• More examples on find upper lower quartile and range
• Practice problems on median, lower quartile, upper quartile and range

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.