FIND THE LOWER QUARTILE UPPER QUARTILE AND INTERQUARTILE RANGE

For each of the following data sets, make sure the data is ordered and then find :

i) the median

ii) the upper and lower quartiles

iii) the range

iv) the interquartile range.

Example 1 :

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

Solution :

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

(i)  The given data is already arranged. 

Number of data values  =  23

Median(Q₂) =  (23+1)/2 ^th value

=  12th value

Median  =  9

(ii)

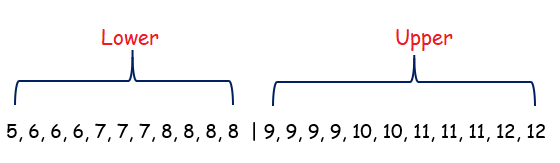
By ignoring the median, we will divide the entire data set into two parts.

Lower quartile :

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8,

Middle value of lower half  =  7

Lower quartile(Q₁)  =  7

Upper quartile :

9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

Middle value of upper half  =  10

Upper quartile(Q₃)  =  10

(iii)  Range  =  Large value - small value

=  12-5

=  7

So, range is 7.

(iv)   Interquartile range :

IQR  =  10-7

IQR  =  3

Example 2 :

11, 13, 16, 13, 25, 19, 20, 19, 19, 16, 17, 21, 22, 18, 19, 17, 23, 15

Solution :

By arranging the data values from least to greatest.

11, 13, 13, 15, 16, 16, 17, 17, 18, 19, 19, 19, 19, 20, 21, 22, 23, 25

(i)  Number of data values  =  18

Median  =  (9^th value + 10^th value)/2

=  (18+19)/2

=  18.5

Median(Q₂)  =  18.5

Note :

Since we don't find median value in the given data set, we divide the data set into two parts without ignoring the median.

(ii)

Lower :  

11, 13, 13, 15, 16, 16, 17, 17, 18

Middle value of lower half  =  16

Lower quartile(Q₁)  =  16

Upper :  

19, 19, 19, 19, 20, 21, 22, 23, 25

Middle value of upper half  =  20

Upper quartile(Q₃)  =  20

(iii)  Range 

Range  =  Large value - small value

=  25-11

=  14

So, range is 14.

(iv)   Interquartile range :

IQR  =  20-16

IQR  =  4

Example 3 :

23.8, 24.4, 25.5, 25.5, 26.6, 26.9, 27, 27.3, 28.1, 28.4, 31.5

Solution :

It is already arranged.

23.8, 24.4, 25.5, 25.5, 26.6, 26.9, 27, 27.3, 28.1, 28.4, 31.5

(i)  Number of data values  =  11

Median  =  (11+1)/2

=  6^th value

Median(Q₂)  =  26.9

(ii)

Lower :  

23.8, 24.4, 25.5, 25.5, 26.6

Middle value of lower half  =  25.5

Lower quartile(Q₁)  =  25.5

Upper :  

 27, 27.3, 28.1, 28.4, 31.5

Middle value of upper half  =  28.1

Upper quartile(Q₃)  =  28.1

(iii)  Range :

=  Large value - small value

=  31.5 - 23.8

=  7.7

So, range is 7.7.

(iv)   Interquartile range :

IQR  =  28.1-25.5

IQR  =  2.6

Example 4 :

The time spent( in minutes) by 24 people in a queue at a supermarket, waiting to be served at the checkout, has been recorded as follows.

1.4    5.2   2.4   2.8   3.4   3.8   2.2   1.5

0.8   0.8    3.9    2.3    4.5   1.4    0.5    0.1

1.6    4.8    1.9     0.2    3.6    5.2    2.7    3.0

a)  Find the median time and the upper and lower quartiles 

b)  Find the range and interquartile range of the waiting time.

c)  Copy and complete the following statements 

i) 50% of the waiting times were greater than ______ minutes.

ii)  75% of the waiting times were less than ______ minutes.

Solution :

a)  Arrange from least to greatest,

0.1   0.2  0.5   0.8   0.8   1.4    1.4    1.5

  1.6   1.9  2.2    2.3   2.4   2.7   2.8    3.0

   3.4  3.6    3.8    3.9   4.5    4.8    5.2    5.2

Total number of terms = 24

Median = [(N/2)th term + (N/2) + 1^th term]/2

= (12th term + 13th term)/2

= (2.3 + 2.4)/2

= 4.7/2

= 2.35

So, the median is 2.35.

b)  Range = 5.1

Interquartile range = 2.3

i) 50% of the waiting times were greater than  2.35 minutes.

ii)  75% of the waiting times were less than 3.7 minutes.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.