DETERMINE WHETHER EACH PAIR OF TRIANGLES IS CONGRUENT

Questions 1-6 : Consider the given pairs of triangles and say whether each pair of triangles are congruent. If the triangles are congruent, say ‘how’ ; if they are not congruent say ‘why’ and also give a small modification would make them congruent :

Question 1 :

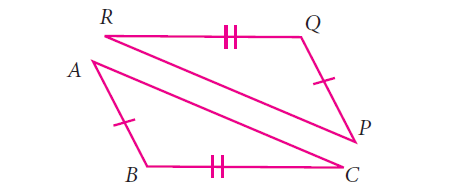
Answer :

In triangle ABC and triangle PQR

AB  =  QP 

BC  =  RQ

From the given information, the triangles are not congruent. If AC and RP were equal, then both the triangles will be congruent by using SSS criterion.

Question 2 :

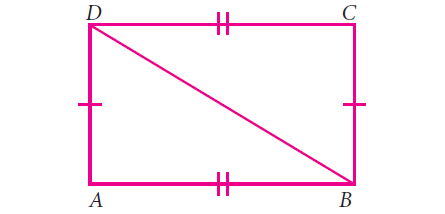
Answer :

In triangle ABD, in triangle BDC

AB  =  DC (S)

AD  =  BC (S)

DB  =  DB (S)

Hence the triangle ABD and BDC are congruent using the criterion SSS.

Question 3 :

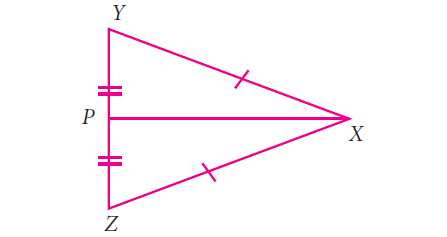
Answer :

In triangle TXP and PXZ

YX  =  ZX  (S) 

YP  =  PZ (S)

PX   =  PX (S)

Hence the triangles TXP and PXZ are congruent using the criterion SSS.

Question 4 :

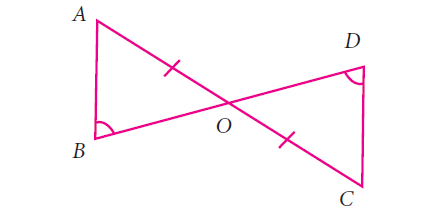
Answer :

In triangle ABO and ODC

AO  =  OC (S)

<ABO  =  <ODC  (A) 

<AOB  =  <DOC  (A)

By using the criterion ASA triangle ABO and ODC are congruent.

Question 5 :

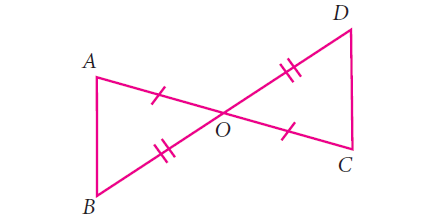
Answer :

In triangle AOB, triangle ODC

BO  =  DO  (S)

AO  =  OC  (S)

<AOB  =  <ODC  (A)

By using the criterion SAS the triangles are AOB and ODC.

Question 6 :

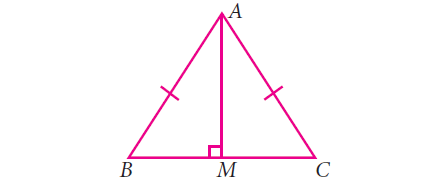
Answer :

In triangle ABM and AMC

AB  =  AC  (S)

<AMB  =  <AMC  (A)

AM  =  AM  (S)

Hence the triangles ABM and AMC are congruent.

Question 7 :

ΔABC and ΔDEF are two triangles in which AB = DF, ∠ACB = 70°, ∠ABC = 60°, ∠DEF = 70° and ∠EDF = 60°. Prove that the triangles are congruent.

Answer :

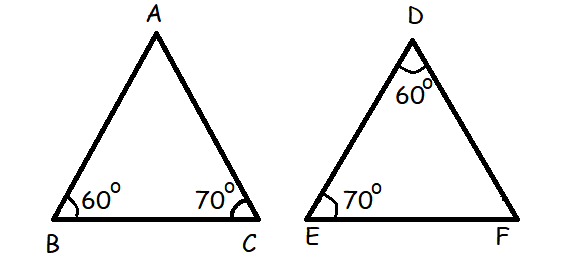
∠ABC  =  ∠EDF  (A) 

∠BCA  =  ∠DEF  (A)

AB  =  EF  (S)

By AAS triangle congruence postulate, the above two triangles are congruent. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.