FUN WITH NUMBERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fun with numbers :
Mathematics is a subject with full of fun, magic and wonders. In this unit, we are going to enjoy with some of this fun and wonder.
Numbers in general form
Let us take the number 42 and write it as
42 = 40 + 2 = 10 × 4 + 2
Similarly, the number 27 can be written as
27 = 20 + 7 = 10 × 2 + 7
In general, any two digit number ab made of digits ‘a’ and ‘b’ can be written as
ab = 10 × a + b = 10a + b
ba = 10 × b + a = 10b + a

Now let us consider the number 351.
This is a three digit number. It can also be written as
351 = 300 + 50 + 1 = 100 × 3 + 10 × 5 + 1 × 1
In general, a 3-digit number abc made up of digit a, b and c is written as
abc = 100 x a + 10 x b + 1 x c
= 100a + 10b + 1c
In the same way, the three digit numbers cab and bca can be written as
cab= 100c + 10a + b
bca = 100b + 10c + a
Games with Numbers
Reversing the digits of a two digit number
Anderson asks David to think of a 2 digit number, and then to do whatever he asks him to do, to that number.
Their conversation is shown in the following figure.
Study the figure carefully before reading on.
Conversation between Anderson and David :
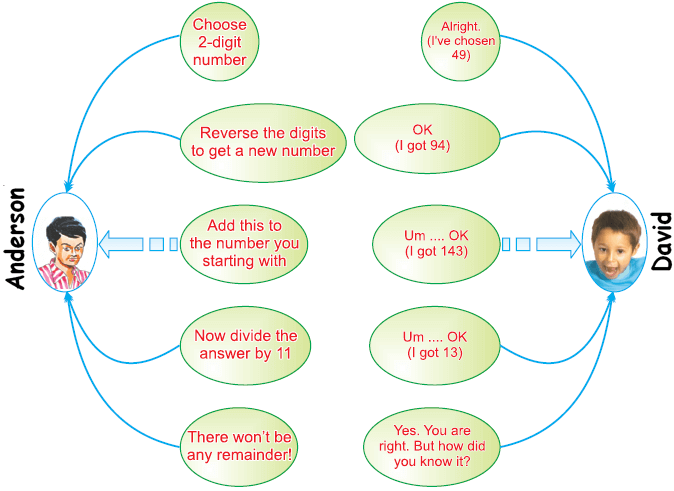
Now let us see if we can explain Anderson's “trick”. Suppose, David chooses the number ab, which is a short form for the 2 -digit number 10a + b. On reversing the digits, he gets the number ba = 10b + a.
When he adds the two numbers he gets :
(10a + b) + (10b + a) = 11a + 11b
= 11(a + b)
So the sum is always a multiple of 11, just as Anderson had claimed.
Dividing the answer by 11, we get (a + b)
(i.e.) Simply adding the two digit number.
Identify the pattern and find the next three terms
Study the pattern in the sequence.
(i) 3, 9, 15, 21, (Each term is 6 more than the term before it)
If this pattern continues, then the next terms are ___ , ___ and ___ .
(ii) 100, 96, 92, 88, ___ , ___ , ___ . (Each term is 4 less than the previous term )
(iii) 7, 14, 21, 28, ___ , ___ , ___ . (Multiples of 7)
(iv) 1000, 500, 250, ___ , ___,___. (Each term is half of the previous term)
(v) 1, 4, 9, 16, ___ , ___ , ___ . (Squares of the Natural numbers)
Number patterns in Pascal’s Triangle
The triangular shaped, pattern of numbers given below is called Pascal’s Triangle.
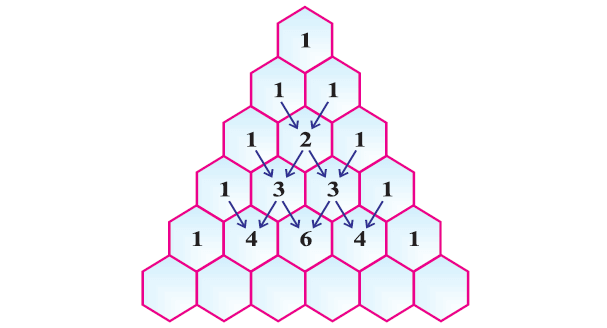
Activity :
Identify the number pattern in Pascal’s triangle and complete the 6th row.
3 × 3 Magic Square
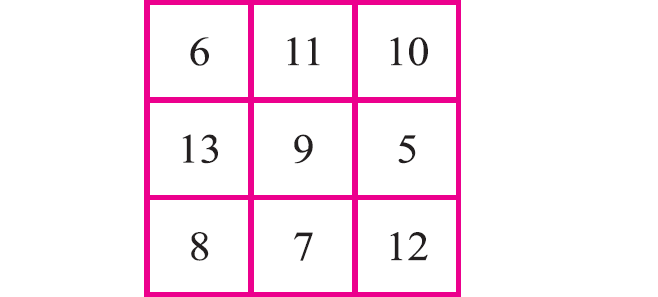
Look at the above table of numbers. This is called a 3 x 3 magic square. In a magic square, the sum of the numbers in each row, each column, and along each diagonal is the same.
In this magic square, the magic sum is 27. Look at the middle number. The magic sum is 3 times the middle number. Once 9 is filled in the center, there are eight boxes to be filled. Four of them will be below 9 and four of them above it.
They could be,
(a) 5, 6, 7, 8 and 10,11,12,13 with a difference of 1 between each number.
(b) 1, 3, 5, 7 and 11,13,15,17 with a difference of 2 between them or it can be any set of numbers with equal differences such as - 11,- 6,- 1, 4 and 14,19, 24, 29 with a difference of 5.
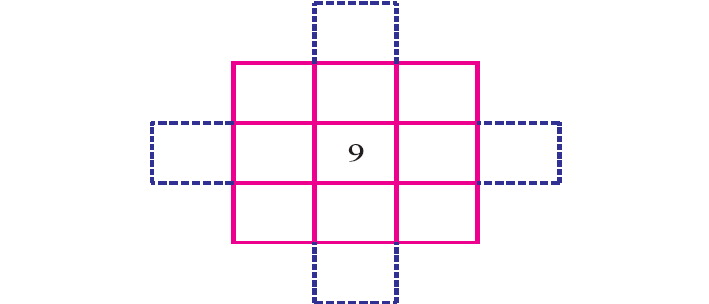
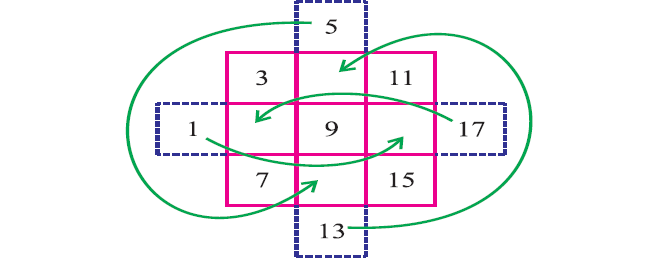
Once we have decided on the set of numbers, say 1, 3, 5, 7 and 11,13,15,17 draw four projections out side the square, as shown in the figures given below and enter the numbers in order, as shown in a diagonal pattern.
The number from each of the projected box is transferred to the empty box on the opposite side.

The Revolving Number
1 4 2 8 5 7
First set out the digits in a circle as given below.
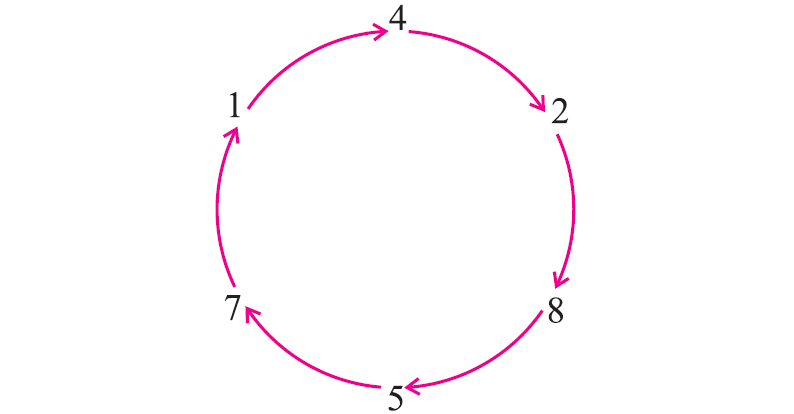
Now multiply 142857 by the number from 1 to 6 as given below.

We observe that the number starts revolving the same digits in different combinations. These numbers are arrived at starting from a different point on the circle.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 29)
Mar 01, 26 07:26 PM
Digital SAT Math Problems and Solutions (Part - 29) -
Digital SAT Math Problems and Solutions (Part - 28)
Mar 01, 26 06:25 PM
Digital SAT Math Problems and Solutions (Part - 28) -
Digital SAT Math Problems and Solutions (Part -27)
Feb 28, 26 07:46 PM
Digital SAT Math Problems and Solutions (Part -27)