FRACTIONS WORKSHEET

Question 1 :

Classify the values given below as proper fraction, improper fraction and mixed fraction. 

⅔, ⁵⁄₂, 5½, ⅞, 0.2, 1.3

Question 2 :

Write down five fractions equivalent to ⅔.

Question 3 :

Evaluate :

²⁄₇ + ³⁄₇

Question 4 :

Evaluate :

⁷⁄₉ - ⁵⁄₉

Question 5 :

Evaluate :

⅛ + ⅝ - ⅜

Question 6 :

Evaluate :

¼ + ⅙

Question 7 :

Evaluate :

⅚ x ⁸⁄₁₁

Question 8 :

Evaluate :

⅔ x ⁵⁄₇

Question 9 :

Evaluate :

⅜ ÷ ¹⁵⁄₁₆

Question 10 :

Write down 1¾ in five different ways, including at least one improper fraction.

Question 11 :

Share a chocolate bar with 32 pieces, equally between four friends. Write down the fraction they each receive in five different ways.

Question 12 :

Write 7 as a fraction in five different ways.

Question 13 :

How many thirds make 5 whole ones?

Question 14 :

Convert the mixed fraction 2⅗ to an improper fraction.

Question 15 :

Convert the improper fraction ¹⁷⁄₅ to a mixed fraction.

Question 16 :

Represent the following fractions on a number line.

⅗, ¹¹⁄₁₂ and ⁷⁄₁₀

Question 17 :

In a fraction, the numerator is 2 less than the denominator. Increasing both numerator and denominator of the fraction by 3 results ⁵⁄₇. Find the fraction.

Question 18 :

James gave one-fourth of a pizza to his brother and gave one-fifth of the remaining to his friend and kept the rest for himself. What fraction of the pizza did James keep for himself?

Answers

1. Answer :

⅔, ⁵⁄₂, 5½, ⅞, 0.2, 1.3

⅔ -----> Proper fraction

⁵⁄₂ -----> Improper fraction

5½ -----> Mixed fraction

⅞ -----> Proper fraction

0.3 = ³⁄₁₀ -----> Proper fraction  

1.3 = ¹³⁄₁₀ -----> Improper fraction

2. Answer :

Multiply the numerator and denominator of the fraction ⅔ by 2, 3, 4, 5 and 6 to get five fractions which are equivalent to 2/3.

3. Answer :

= ²⁄₇ + ³⁄₇

Since the above two fractions have the same denominator, the denominator can be taken once and add the numerators.

= ⁽² ⁺ ³⁾⁄₇

= ⁵⁄₇

4. Answer :

= ⁷⁄₉ - ⁵⁄₉

Since the above two fractions have the same denominator, the denominator can be taken once and subtract numerators.

= ⁽⁷ ⁻ ⁵⁾⁄₉

= ²⁄₉

5. Answer :

= ⅛ + ⅝ - ⅜

Since the above fractions have the same denominator, the denominator can be taken once and combine the numeartors.

= ⁽¹ ⁺ ⁵ ⁻ ³⁾⁄₈

= ⅜

6. Answer :

= ¼ + ⅙

The above fractions do not have the same denominator. 

Find the least common multiple of the denominators 4 and 6.

Least common multiple of the denominators (4, 6) is 12.

Make the denominators of both the fractions as 12 by multiplying the numerators and denominators by appropriate numbers

= ⁽¹ˣ³⁾⁄₍₄ₓ₃₎ + ⁽¹ˣ²⁾⁄₍₆ₓ₂₎

= ³⁄₁₂ + ²⁄₁₂ 

Now, the above two fractions have the same denominator. So, the denominator can be taken once and combine the numeartors.

= ³⁄₁₂ + ²⁄₁₂

= ⁽³ ⁺ ²⁾⁄₁₂

= ⁵⁄₁₂

7. Answer :

= ⅚ x ⁸⁄₁₁

The denominator of the first fraction 6 and the numerator of the second fraction 8 have the common divisor 2. So, divide 6 and 8 by 2. (Note : This kind of division can be done only with numerator and denomiator, not with numerator and numerator or denominator with denominator).

= ⁵⁄₃ x ⁴⁄₁₁

Multiply the numerators and denominators.

= ²⁰⁄₃₃

8. Answer :

= ⅔ x ⁸⁄₇

Here, there is no common divisor for any numerator and any denominator. So, multiply the numerators and denominators.

= ¹⁶⁄₂₁

9. Answer :

= ⅜ ÷ ¹⁵⁄₁₆

Change the division to multiplication and take reciprocal for the second fraction ¹⁵⁄₁₆.

= ⅜ x ¹⁶⁄₁₅

Simplify.

= ¹⁄₁ x ⅖

Multiply the numerators and denominators.

= ⅖

10. Answer :

Multiply the numerator and denominator of the fractional part of 1¾ by 2, 3, 4, and 5 to write down 1¾ in four different ways.

To get an improper fraction which is equivalent to 1¾, multiply the whole number 1 by the denominator 4 then add the numerator before writing it all over the denominator.

In this way, we can write down 1¾ in five different ways, including at one improper fraction as shown below.

11. Answer :

A chocolate bar is divided into 32 pieces and those 32 pieces are divided among four friends.

Number of pieces each friend gets : 

= 32 ÷ 4

= 8

Each friend gets 4 out of 32 pieces.

= 8 ÷ 32

= ¼

Each friend gets ⅛ part of the chocolate bar.

We can multiply the numerator and denominator of the fraction ¼ by 2, 3, 4, 5 and 6 to write down the fraction they each receive in five different ways.

12. Answer :

We can write any integer as a fraction by taking the denominator as 1.

So, the first way to write 7 as a fraction is ⁷⁄₁.

Further, we can multiply the numerator and denominator of the fraction ⁷⁄₁ by 2, 3, 4 and 5 to write ⁷⁄₁ in four more different ways.

In this way, we can write 7 as a fraction in five different ways as shown below.

13. Answer :

One third = ⅓

We need 3 thirds to make 1 whole one.

1 whole one = 3 thirds

5 whole ones = 5(3 thirds)

= 15 thirds

15 thirds make 5 whole ones.

14. Answer :

We can convert the mixed fraction 2⅗ to an improper fraction as shown below.

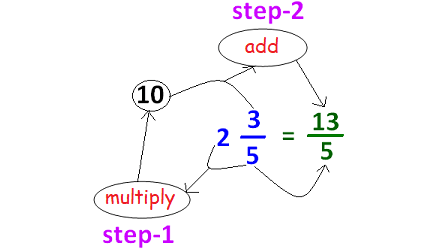
2⅗ = 13/5

15. Answer :

We can convert the improper fraction 17/5 to a mixed fraction as shown below.

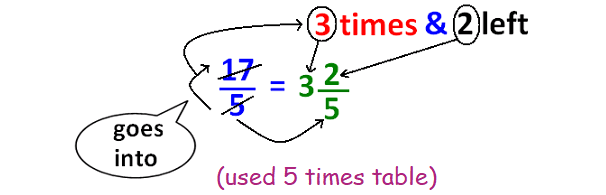
¹⁷⁄₅ = 3⅖

16. Answer :

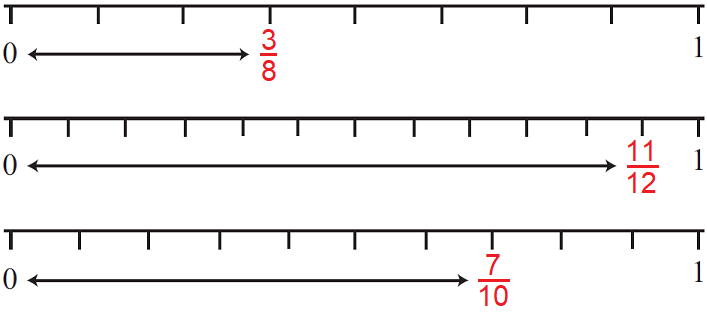
17. Answer :

Let x be the denominator.

Given : The numerator of the fraction is 2 less than the denominator.

Then, the fraction is

= ⁽ˣ ⁻ ²⁾⁄ₓ ----(1)

Given : Increasing both numerator and denominator of the fraction by 3 results ⁵⁄₇.

⁽ˣ ⁻ ² ⁺ ³⁾⁄₍ₓ ₊ ₃₎ = ⅘

⁽ˣ ⁺ ¹⁾⁄₍ₓ ₊ ₃₎ = ⅘

5(x + 1) = 4(x + 3)

5x + 5 = 4x + 12

x + 5 = 12

x = 7

Substitute x = 7 in (1).

fraction = ⁽⁷ ⁻ ²⁾⁄₇

= ⁵⁄₇

18. Answer

Amount of pizza left after James gave ¼ of it to his brother :

= ¾

Amount of pizza james gave his friend :

= ⅕ of ¾

= ⅕ x ¾

= ³⁄₂₀

Fraction of pizza James kept for himself :

= 1 - ¼ - ³⁄₂₀

= ²⁰⁄₂₀ - ⁵⁄₂₀ - ³⁄₂₀

= ⁽²⁰ ⁻ ⁵ ⁻ ³⁾⁄₂₀

= ¹²⁄₂₀

= ⅗

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.