FINDING PERCENT CHANGE

Percents can be used to describe how an amount changes. The formula given below can be used to find how an amount changes in terms of percentage. 

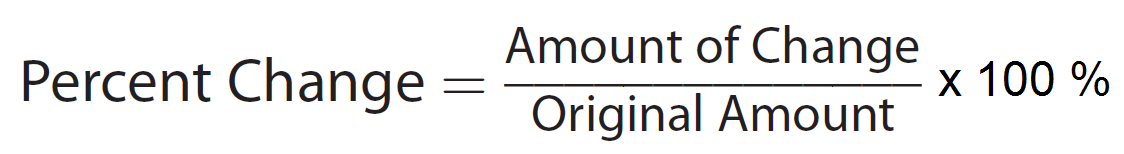
The change may be an increase or a decrease.

Percent increase describes how much a quantity increases in comparison tothe original amount.

Percent decrease describes how much a quantity decreases in comparison to the original amount.

Examples

Example 1 : 

The price of an item was original priced $40. Due to increase in demand, the price is increased to $50. By what percentage is the price increased ?

Solution :

Amount of change :

=  50 - 40

=  $10

Percentage change is 

=  (Amount of change / Original amount) ⋅ 100 %

=  (10 / 40) ⋅ 100%

=  25%

So, the price of the item is increased by 25%.

Example 2 : 

The price of an item is $60. After negotiation, Michael buys the item for $51. By what percentage is the price of the item decreased ? 

Solution :

Amount of change :

=  60 - 51

=  $9

Percentage change is 

=  (Amount of change / Original amount) ⋅ 100 %

=  (9 / 60) ⋅ 100%

=  15%

So, the price of the item is decreased by 15%. 

Example 3 : 

In a software company, initially a fresher takes 40 days to complete a job. After one year experience, if the same person completes the same type of job in 4 weeks, find the percentage change in time taken to complete the job.  

Solution :

No. of days initially taken to complete the job is 40. 

After one year experience, time taken to complete the same job is

=  4 weeks 

=  4 ⋅ 7 days

=  28 days

Difference in time taken to complete the job :

=  40 - 28

=  12 days

Percentage change is 

=  (12 / 40) ⋅ 100 %

=  30%

So, the percentage change in time taken to complete the job is 30.

Example 4 : 

In a school, there were 13 boys and 12 girls in a class in the last academic year. If 4 new boys and 6 new girls are admitted in this academic year, find the percentage change in class strength.

Solution :

Total number of students in the last academic year was

=  13 + 12

=  25

Students' strength details in this academic year : 

No. of boys  =  13 + 4  =  17

No. of girls  =  12 + 6  =  18

Total number of students in this academic year is 

=  17 + 18

=  35

Difference in class strength between last year and this year is 

=  35 - 25

=  10

Percentage change is 

=  (10 / 25) ⋅ 100 %

=  40%

So, the percentage change in class strength is 40.

Example 5 : 

Lily was working 5 hours per day and 4 days in a week. She gets a raise, and her hourly wage increased from $8 to $10. If she works for 8 hours per day and 5 days in a week in the new wage, find the percent change in her earning per week ?

Solution :

When Lily worked 5 hours per day and 4 days in a week, her weekly earning was

=  5 ⋅ 8 ⋅ 4

=  $160

When Lily works 8 hours per day and 5 days in a week, her earning weekly is 

=  8 ⋅ 10 ⋅ 5

=  $400

Increase in earning : 

=  400 - 160

=  $240

Percent change in earning per week is 

=  (240 / 160) ⋅ 100%

=  150%

So, the percent change in Lily's earning per week is 150%.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.