FIND TRIGONOMETRIC RATIOS USING RIGHT TRIANGLES

Example 1 :

In the right triangle shown below, find the six trigonometric ratios of the angle θ. 

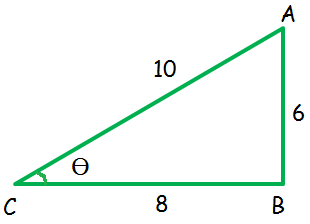
Solution :

From the above triangle, we come to know that the right angled at B.

AC - hypotenuse  =  10

AB - opposite side  =  6 

BC - Adjacent side  =  8

Finding the vale of sin θ :  

sin θ  =  Opposite side/Hypotenuse

sin θ  =  AB/AC

sin θ  =  6/10

sin θ  =  3/5

Finding the vale of cos θ :  

cos θ  =  Adjacent side/Hypotenuse

cos θ  =  BC/AC

cos θ  =  8/10

cos θ  =  4/5

Finding the vale of tan θ :

tan θ  =  Opposite side/Adjacent side 

tan θ  =  AB/BC

tan θ  =  6/8

tan θ  =  3/4

Finding the vale of csc θ :  

csc θ = Hypotenuse /Opposite side

csc θ  =  AC/AB

csc θ  =  10/6

csc θ  =  5/3

Finding the vale of sec θ :  

sec θ = Hypotenuse /Adjacent side

sec θ  =  AC/BC

sec θ  =  10/8

sec θ  =  5/4

Finding the vale of cot θ :  

cot θ = Adjacent side/opposite side

cot θ  =  BC/AB

cot θ  =  8/6

cot θ  =  4/3

Example 2 :

In the right triangle shown below, find the six trigonometric ratios of the angle θ. 

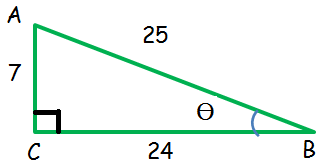
Solution :

In the triangle above, right angle is at C.

AB - hypotenuse = 25

AC - opposite side = 7 

BC - Adjacent side = 24

Finding the vale of sin θ :  

sin θ  =  Opposite side/Hypotenuse side 

sin θ  =  AC/AB

sin θ  =  7/25

Finding the vale of cos θ :  

cos θ  =  Adjacent side/Hypotenuse side 

cos θ  =  BC/AB

cos θ  =  24/25

Finding the vale of tan θ :  

tan θ  =  Opposite side/Adjacent side 

tan θ  =  AC/BC

tan θ  =  7/24 

Finding the vale of csc θ :  

csc θ  =  Hypotenuse /Opposite side

csc θ  =  AB/AC

csc θ  =  25/7 

Finding the vale of sec θ :  

sec θ  =  Hypotenuse /Adjacent side

 sec θ  =  AB/BC

sec θ   =  25/24

Finding the vale of cot θ :  

cot θ  =  Adjacent side/opposite side

cot θ  =  BC/AC

cot θ  =  24/7

Example 3 :

In the right triangle shown below, find the six trigonometric ratios of the angle θ. 

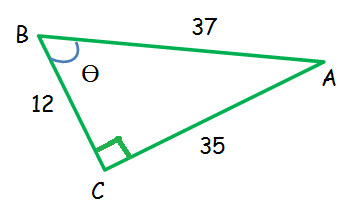
Solution :

From the above triangle right angled at C.

AB - hypotenuse = 37

AC - opposite side = 35 

BC - Adjacent side = 12

Finding the vale of sin θ : 

sin θ  =  Opposite side/Hypotenuse

sin θ  =  AC/AB

sin θ  = 35/37

Finding the vale of cos θ : 

cos θ  =  Adjacent side/Hypotenuse

cos θ  =  BC/AB

cos θ  =  12/37

Finding the vale of tan θ :

tan θ  =  Opposite side/Adjacent side

tan θ  =  AC/BC

tan θ  =  35/12 

Finding the value of csc θ : 

csc θ  =  Hypotenuse /Opposite side

csc θ  =  AB/AC

csc θ  =  37/35 

Finding the value of sec θ : 

sec θ  =  Hypotenuse/Adjacent side

sec θ  =  AB/BC

sec θ  =  37/12

Finding the value of cot θ : 

cot θ  =  Adjacent side/opposite side

cot θ  =  BC/AC

cot θ  =  12/35

Example 4 :

Given right angle shown, represent the value of tan A

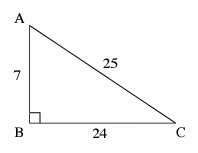
Solution :

AC - Hypotenuse

The side which is opposite to ∠A is opposite side. In this way, 

AB = Opposite side and BC = adjacent side

tan A = Opposite side / Adjacent side

tan A = AB / BC

tan A = 7/24

Example 5 :

Given right angle shown, represent the value of cos Q

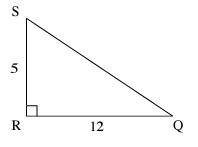
Solution :

Hypotenuse = SQ, opposite side = SR = 5 and adjacent side = 12

SQ² = RS² + RQ²

SQ² = 5² + 12²

= 25 + 144

= 169

SQ = √169

SQ = 13 = Hypotenuse

cos Q = Adjacent side / Hypotenuse

cos A = 12/13

Example 6 :

If sin x = 1/3, what is the value of cos x ?

Solution :

sin x = 1/3

To figure out the value of cos x, we need adjacent side.

Opposite side = 1x, hypotenuse = 3x

Adjacent side = ?

(Hypotenuse)² = (Opposite side)² + (Adjacent side)²

(3x)² = (1x)² + (Adjacent side)²

9x² - 1x² = Adjacent side²

Adjacent side² = 8x²

Adjacent side = √8x²

= 2x√2

cos x = Adjacent side / Hypotenuse

= 2x√2 / 3x

= 2√2/3

Example 7 :

Given the right triangle ABC above, which of the following is equal to a/c ?

I. sin A         II. cos B        III. tan A

A) I only     B) II only 

 C) I and II only      D)  II and III only

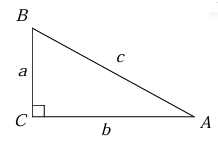
Solution :

Considering angle measure in A, we get 

a = opposite side, b = adjacent side and c - Hypotenuse

a/c = Opposite side / Hypotenuse

a/c = tan A

Considering angle measure in B, we get 

b = opposite side, a = adjacent side and c - Hypotenuse

a/c = adjacent side / Hypotenuse

a/c = cos B

By observing the options II and III are correct. So, option D is correct.

Example 8 :

In the triangle shown below AB = BC = 10 cm and AC = 12 cm.

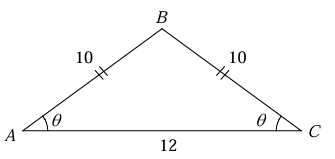
What is the value of sin θ ?

Solution :

Angle measure B is 90 degree.

sin θ = Opposite side / hypotenuse

Opposite side = 10, adjacent = 10 and hypotenuse = 12

sin θ = 10/12

sin θ = 5/6

Example 9 :

In the triangle shown below AB = BC = 10 cm and AC = 12 cm.

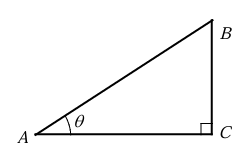
In the triangle shown above, if tan A = 3/4, what is sin θ

Solution :

tan A = 3/4 = Opposite side / Adjacent side

Let 3x and 4x are the measures of opposite side and adjacent side respectively.

(Hypotenuse)² = (Opposite side)² + (Adjacent side)²

AB² = (3x)² + (4x)²

= 9x² + 16x²

= 25x²

AB = 5x

sin θ = Opposite side / hypotenuse

= 3x/5x

sin θ = 3/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.