FIND THE MISSING SIDE OF A TRIANGLE USING THE PYTHAGOREAN THEOREM

In any right angled triangle, the length of square of hypotenuse is equal to the sum of the squares on the other two sides

In a right angled triangle, with hypotenuse c and legs a and b,

c² = a² + b²

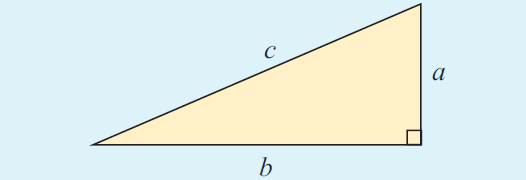
Find the value of unknowns.

Example 1 :

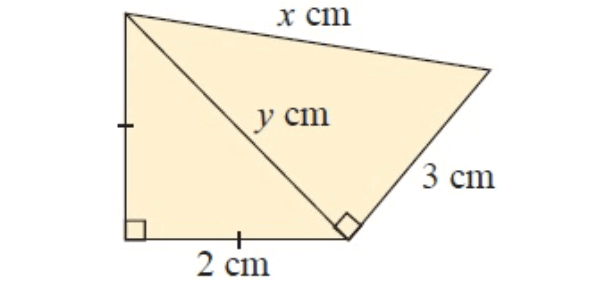
Solution :

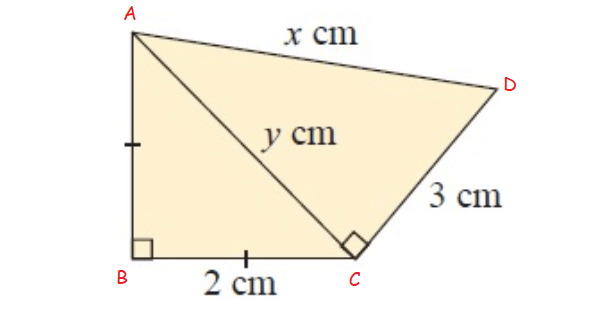
In figure ∆ABC and ∆ACD

In ∆ABC,

AB  =  2 cm, BC  =  2 cm and AC  =  y cm

By using Pythagorean theorem,

AB² + BC²  =  AC²

2² + 2²  =  y²

4 + 4  =  y²

y²  =  8

In ∆ACD,

AC  =  y cm, CD  =  3 cm and AD  =  x cm

AC² + CD²  =  AD²

y² + 3²  =  x²

8 + 9  =  x²

x²  =  17

Now,

x  =  √17 and y  =  √8

x  =  4.12 cm and y  =  2.8 cm

Example 2 :

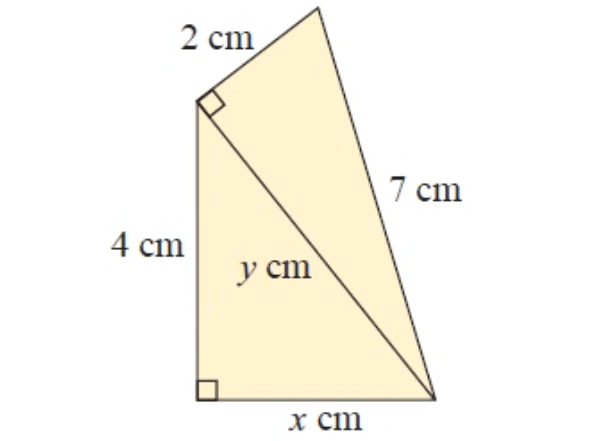
Solution :

In figure ∆ABC and ∆DAC

In ∆ABC,

AB  =  4 cm, BC  =  x cm and AC  =  y cm

By using Pythagorean theorem,

AB² + BC²  =  AC²

4² + x²  =  y²

16 + x²  =  y²

x²  =  y² – 16 -----(1)

In ∆DAC,

DA  =  2 cm, AC  =  y cm and DC  =  7 cm

DA² + AC²  =  DC²

2² + y²  =  7²

4 + y²  =  49

y²  =  49 – 4

y²  =  45 -----(2)

By applying, y²  =  45 in (1)

We get,

x²  =  y² – 16

=  45 – 16

x²  =  29

x  =  √29 and y  =  √45

x  =  5.38 and y  =  6.70

Example 3 :

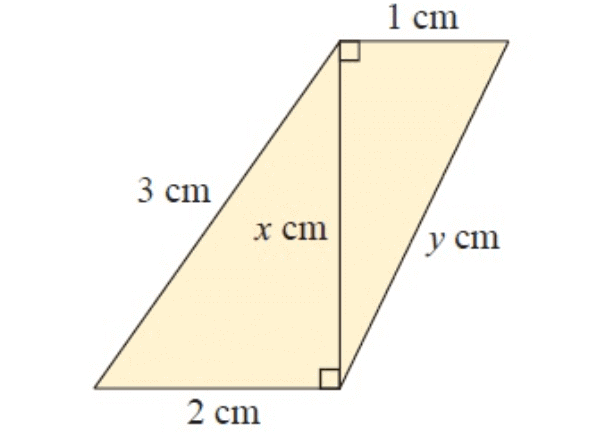
Solution :

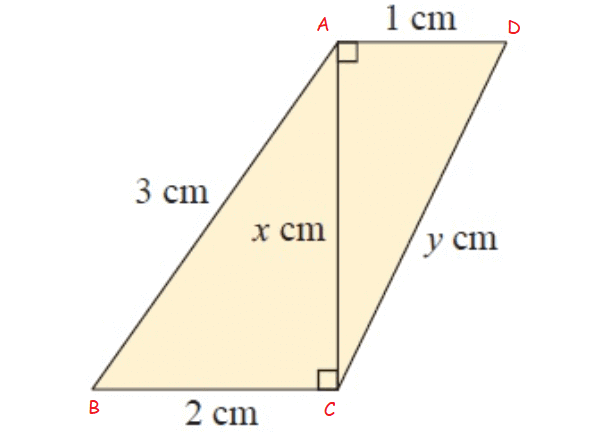
In figure ∆ACB and ∆DAC

In ∆ACB,

AC  =  x cm, BC  =  2 cm and AB  =  3 cm

By using Pythagorean theorem,

AC² + BC²  =  AB²

x² + 2²  =  3²

x² + 4  =  9

x²  =  5

In ∆DAC,

DA  =  1 cm, AC  =  x cm and DC  =  y cm

DA² + AC²  =  DC²

1² + x²  =  y²

1 + 5  =  y²

y²  =  6

x  =  √5 and y  =  √6

x  =  2.23 and y  =  2.44

Example 4 :

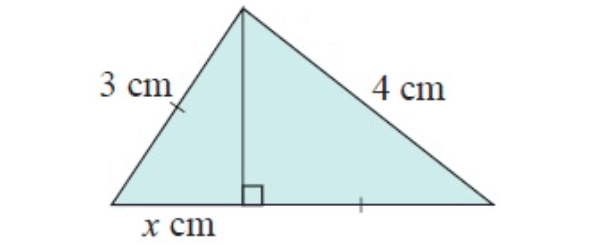
Solution :

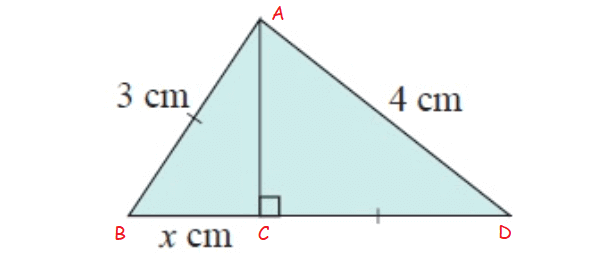
In figure ∆ACB and ∆ACD

In ∆ACB,

AC  =  ?, BC  =  x cm and AB  =  3 cm

By using Pythagorean theorem,

AC²+BC²  =  AB²

AC²+x²  =  3²

AC²  =  9–x² -----(1)

In ∆ACD,

AC  =  ?, CD  =  3 cm and AD  =  4 cm

AC²+CD²  =  AD²

AC²+3²  =  4²

AC²  =  7 -----(2)

By applying, AC²  =  7 in (1)

AC²  =  9–x²

7  =  9–x²

x²  =  9–7

x²  =  2

x  =  √2

x  =  1.414 

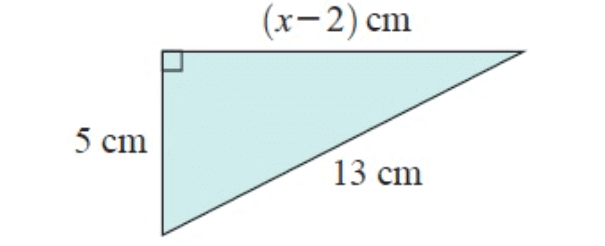
Example 5 :

Solution :

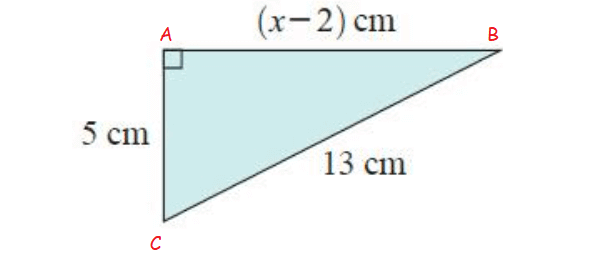
In figure ∆ABC

In ∆ABC,

AB  =  (x – 2) cm, BC  =  5 cm and AC  =  13 cm

By using Pythagorean theorem,

AB² + BC²  =  AC²

(x–2)²+5²  =  13²

x²–4x+4+25  =  169

x²–4x+29–169  =  0

x²–4x–140  =  0

By factorization, we get

(x + 10) (x – 14)  =  0

x  =  - 10 and 14

Now, taking positive value 14.

So, the value of x is 14 cm.

Example 6 :

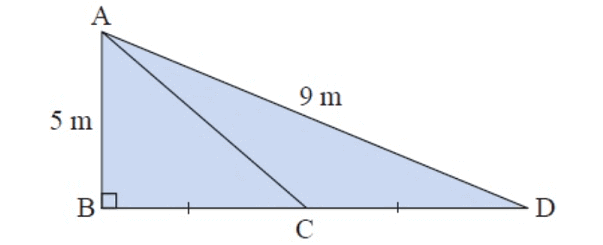
Solution :

In figure ∆ABC and ∆ABD

In ∆ABC,

AB  =  5 m, let BC  =  x m and AC  =  ?

By using Pythagorean theorem,

AB² + BC²  =  AC²

5² + x²  =  AC²

25 + x²  =  AC²

AC²  =  25 + x² -----(1)

In ∆ABD,

AB  =  5 m, AD  =  9 m

BD  =  BC + CD

=  x + x

=  (2x) m

AB² + BD²  =  AD²

5² + (2x)²  =  9²

25 + 4x²  =  81

4x²  =  81 – 25

4x²  =  56

x²  =  56/4

x²  =  14 -----(2)

By applying, x²  =  14 in (1)

AC²  =  25 + x²

AC²  =  25 + 14

AC²  =  39

Now,

AC  =  √39

AC  =  6.24

We taking this value Approximately,

So, the Length of AC is 6 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.