FIND THE LENGTH OF HYPOTENUSE OF A RIGHT TRIANGLE

In any right angled triangle, the length of square of hypotenuse is equal to the sum of the squares on the other two sides

In a right angled triangle, with hypotenuse c and legs a and b,

c² = a² + b²

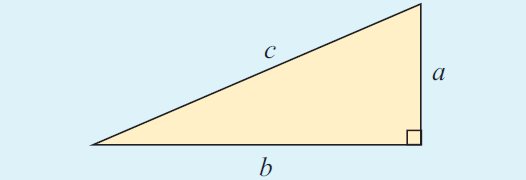
Find the length of hypotenuse :

Example 1 :

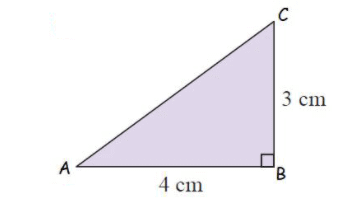
Solution :

By using Pythagoras theorem,

AB² + BC²  =  AC²

4² + 3²  =  AC²

9 + 16  =  AC²

25  =  AC²

AC  =  √25

AC  =  5 cm

So, length of the hypotenuse is 5cm.

Example 2 :

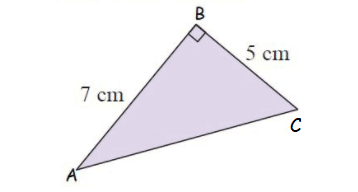
Solution :

By using Pythagoras theorem,

AB² + BC²  =  AC²

7² + 5²  =  AC²

49 + 25  =  AC²

74  =  AC²

AC  =  √74

AC  =  8.6cm

So, length of the hypotenuse is 8.6 cm.

Example 3 :

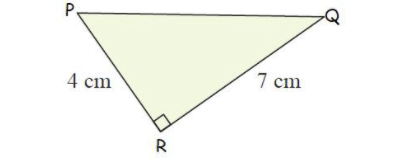
Solution :

By using Pythagoras theorem,

PR² + RQ²  =  PQ²

4²+ 7²  =  PQ²

16 + 49  =  PQ²

65  =  PQ²

PQ  =  √65

PQ  =  8.1 cm

So, length of the hypotenuse is 8.1 cm.

Example 4 :

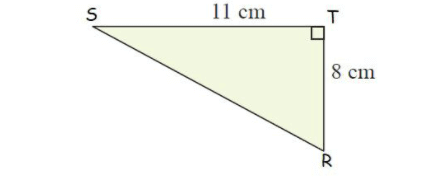
Solution :

By using Pythagoras theorem,

ST² + TR²  =  SR²

11² + 8²  =  SR²

121 + 64  =  SR²

185  =  SR²

SR  =  √185

SR  =  13.6 cm

So, length of the hypotenuse is 13.6 cm.

Example 5 :

The size of a computer monitor is the length across its diagonal. If a computer monitor is 34.4 cm long and 27.5 cm high, what size is it?

Solution :

In figure, given

Height of a computer monitor (a)  =  27.5 cm

Length of base (b)  =  34.4 cm

Let c be the length of diagonal.

By using Pythagoras theorem,

a² + b²  =  c²

(27.5)² + (34.4)²  =  c²

 c²  =  756.25 + 1183.36 

c²  =  1939.61

c  =  √1939.61

c  =  44.0 cm

So, length of the diagonal c is 44.0 cm.

Example 6 :

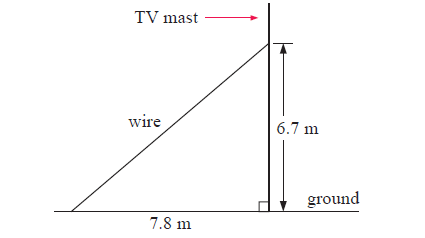
(a)  Find the length of the wire shown supporting the TV mast. 

(b) There are six wires which support the mast.

i)  Find their total length.

ii)  If 3% extra wire is needed for tying, how many meters of wire need to be purchased?

Solution :

(a) By finding length of hypotenuse, we can find the length of wire needed.

In figure, 

a  =  6.7 m and b  =  7.8 m

To find the length of the wire c  =  ?

By using Pythagoras theorem,

(6.7)² + (7.8)²  =  c²

44.89 + 60.84  =  c²

105.73  =  c²

c  =  √105.73

c  =  10.28 m

So, length of the wire c is 10.28 m.

(b)

(i)  Length of the one wire is 10.28 m.

Length of 6 wires  =  10.28 × 6

=  61.68 m

So, total length is 61.7 m

(ii) If 3% extra wire is needed for tying, how many meters of wire need to be purchased? The wire must be purchased in a whole number of meters.

We have already 6 wires.

We need 3% extra wire,

=  6 + 3% of 61.68

=  6.18

So, total wires 6.18

Total meters of wires purchased 

=  Length of the wire × total wires

=  10.28 × 6.18

=  63.53 m

So, 64 m of wire to be purchased.

Example 7 :

Metal supports are made as shown. They are fitted from the lower edge of the table top to the legs. The flat ends of the supports are 2 cm long. Find the length of the metal needed to make the 8 supports used to stabilise the table.

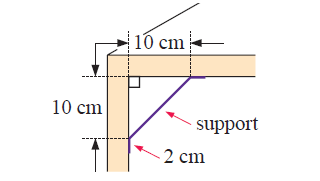
In figure, given

We see this right triangle,

Top metal fits a  =  10 cm

Lower edge metal fits b  =  10 cm

Length of the metal support c  =  ?

By using Pythagoras theorem,

a² + b²  =  c²

10² + 10²  =  c²

100 + 100  =  c²

200  =  c²

c  =  √200

c  =  14.14 cm

Length of the metal supports c  =  14.14 cm

Length of the metal supports 2 cm long top and lower,

So, Length of the metal supports  =  18.14 cm

We need,

Length of the metal 8 supports  =  18.14 × 8

=  145.12 cm

Therefore, Length of the metal 8 supports is  145.12 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.