FIND AREA AND PERIMETER BY COUNTING SQUARES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Find the area of the figure given below.
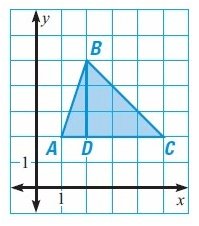
Solution :
By observing the figure, it is a triangle.
Then, AC = base and BD = height
There are 4 units for the base and 3 units for height.
Finding the area :
Area of a triangle = 1/2 × base × height
= 1/2 × 4 × 3
Area = 6 sq.units
Example 2 :
Find the area and perimeter of the figure given below.
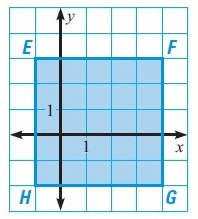
Solution :
By observing the figure, it is a square.
Then, HG = GF = EF = EH = side
There are 5 units for the side.
Finding the area :
Area of a square = side2
= 52
Area = 25 sq.units
Finding the Perimeter :
Perimeter of a square = 4a
= 4(5)
Perimeter = 20 units
Example 3 :
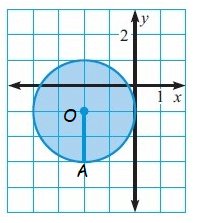
Solution :
By observing the figure, it is a circle.
Then, OA = radius
There are 2 units for radius.
Finding the area :
Area of a circle = πr2
= π(22)
= 4π
Area = 4π sq.units
Draw the figure in a coordinate plane and find its area and perimeter.
Example 4 :
Triangle defined by A(3, 4), B(7, 4), and C(5, 7)
Solution :
By plotting the given points on the graph, we get
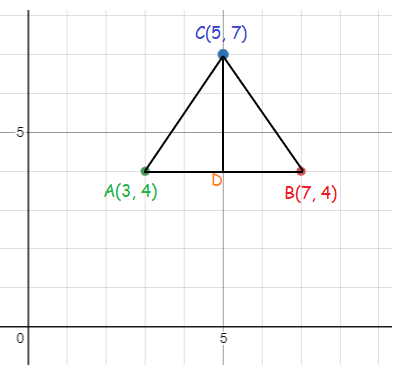
Now, there is a triangle.
Then, AB = base and CD = height
There are 4 units for the base and 3 units for height.
Finding the area :
Area of a triangle = 1/2 × base × height
= 1/2 × 4 × 3
Area = 6 sq.units
Example 5 :
Triangle defined by R(-2, -3), S(6, -3), and T(5, 4)
Solution :
By plotting the given points on the graph, we get
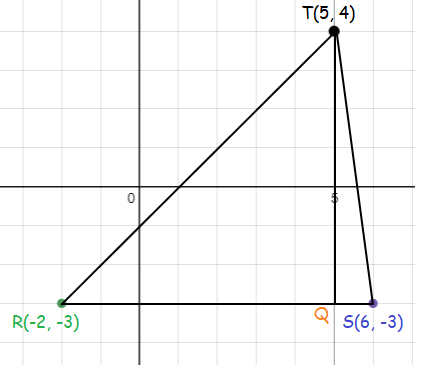
Now, there is a triangle.
Then, RS = base and TQ = height
There are 8 units for the base and 7 units for height.
Finding the area :
Area of a triangle = 1/2 × base × height
= 1/2 × 8 × 7
Area = 28 sq.units
Example 6 :
Rectangle defined by L(-2, -4), M(-2, 1), N(7, 1) and P(7, -4)
Solution :
By plotting the given points on the graph, we get
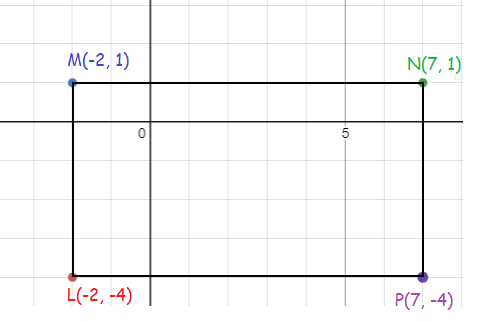
Now, there is a rectangle.
Then, LP = length and NP = width
There are 9 units for the length and 5 units for width.
Finding the area :
Area of a rectangle = length × width
= 9 × 5
Area = 45 sq.units
Finding the perimeter :
Perimeter of a rectangle = 2(length + width)
= 2(9 + 5)
= 2(14)
Perimeter = 28 units
Example 7 :
Square defined by W(5, 0), X(0, 5), Y(-5, 0) and Z(0, -5)
Solution :
By plotting the given points on the graph, we get
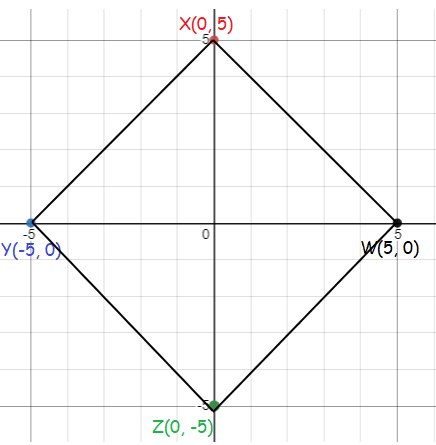
Now, there is a square.
But, we couldn’t calculate XY = YZ (side)
So, we are using the diagonals.
Here, d = 10 units
Finding the area :
Area of square using diagonals = 1/2 × d2
= 1/2 × 102
= 1/2 × 100
Area = 50 sq.units
Finding the perimeter :
Perimeter of a square using diagonals = 4 × √(d2/2)
= 4 × √(102/2)
= 4 × √100/2
= 4 × √50
= 4 × 5√2
= 20√2
Perimeter = 20√2 units
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

