EXPONENTS AND SQUARE ROOTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Exponent :
The exponent of a number says how many the number has to be multiplied by itself.
In 92 the '2' says that 9 has to be used twice twice in multiplication, so 92 = 9 × 9 = 81.
In words : 92 can be called '9 to the power 2' or '9' to the second power, or simply '9 squared' Exponents are also called Powers or Indices.
Square Root :
Square root of a number is a value that can be multiplied by itself to give the original number.
The symbol of the square root is
√
Square root of 9 is 3.
Because when 3 is multiplied by itself, we get 9.
Exponent Rules
Rule 1 :
xm ⋅ xn = xm+n
Rule 2 :
xm ÷ xn = xm-n
Rule 3 :
(xm)n = xmn
Rule 4 :
(xy)m = xm ⋅ ym
Rule 5 :
(x / y)m = xm / ym
Rule 6 :
x-m = 1 / xm
Rule 7 :
x0 = 1
Rule 8 :
x1 = x
Rule 9 :
xm/n = y -----> x = yn/m
Rule 10 :
(x / y)-m = (y / x)m
Rule 11 :
ax = ay -----> x = y
Rule 12 :
xa = ya -----> x = y
Square Root Rules
Rule 1 :
√a ⋅ √b = √(ab)
Rule 2 :
√a / √b = √(a/b)
Rule 3 :
√a⋅ √a = a
Rule 4 :
√a = k -----> a1/2 = k
Rule 5 :
√a = b -----> a = b2
Practice Problems
Problem 1 :
Simplify :
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4)
Solution :
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a7+2-4 / a2-3+4
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a5 / a3
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a5-3
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a2
Problem 2 :
Simplify :
(a6 ⋅ b3) / (a2 ⋅ b-3)2
Solution :
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = (a6 ⋅ b3) / [(a2)2 ⋅ (b-3)2]
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = (a6 ⋅ b3) / (a4 ⋅ b-6)
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = a6-4 ⋅ b3+6
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = a2b9
Problem 3 :
If 82n + 3 = 4n + 5, then find the value of n.
Solution :
82n + 3 = 4n + 5
(23)2n + 3 = (22)n + 5
23(2n + 3) = 22(n + 5)
Equate the exponents.
3(2n + 3) = 2(n + 5)
6n + 9 = 2n + 10
4n = 1
n = 1/4
Problem 4 :
Simplify the following square root expression :
√40 + √160
Solution :
Decompose 40 and 160 into prime factors using synthetic division.
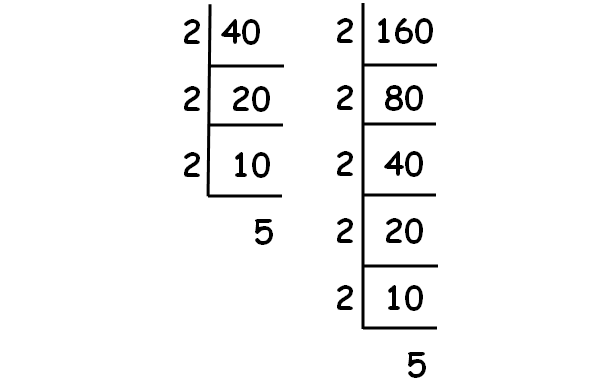
√40 = √(2 ⋅ 2 ⋅ 2 ⋅ 5) = 2√10
√160 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) = 4√10
So, we have
√40 + √160 = 2√10 + 4√10
√40 + √160 = 6√10
Problem 5 :
Simplify the following square root expression :
(14√117) ÷ (7√52)
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
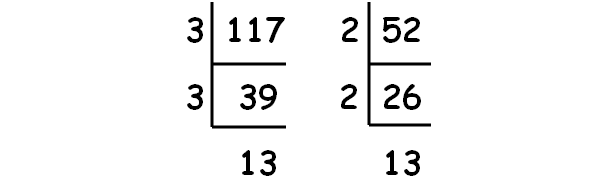
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(14√117) ÷ (7√52) = 14(3√13) ÷ 7(2√13)
(14√117) ÷ (7√52) = 42√13 ÷ 14√13
(14√117) ÷ (7√52) = 42√13 / 14√13
(14√117) ÷ (7√52) = 3
Problem 6 :
Simplify the following square root expression :
(√3)3 + √27
Solution :
(√3)3 + √27 = (√3 ⋅ √3 ⋅ √3) + √(3 ⋅ 3 ⋅ 3)
(√3)3 + √27 = (3 ⋅ √3) + 3√3
(√3)3 + √27 = 3√3 + 3√3
(√3)3 + √27 = 6√3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Practice Test with Answers (Part - 1)
Mar 12, 26 06:55 PM
Digital SAT Math Practice Test with Answers (Part - 1) -
Digital SAT Math Practice Test with Answers (Part - 2)
Mar 12, 26 06:40 PM
Digital SAT Math Practice Test with Answers (Part - 2) -
Digital SAT Math Questions and Answers (Part - 1)
Mar 12, 26 10:06 AM
Digital SAT Math Questions and Answers (Part - 1)