EXAMPLES ON INTERNAL AND EXTERNAL ANGLE BISECTOR THEOREM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Angle Bisector Theorem :
The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle.
To know more about proof, please visit the page "Angle bisector theorem proof".
Example 1 :
In a triangle MNO, MP is the external bisector of
angle M meeting NO produced at P. IF MN = 10 cm, MO = 6 cm, NO - 12 cm,
then find OP.
Solution :
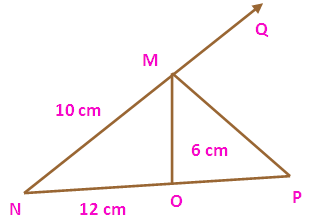
MP is the external bisector of angle M by using angle bisector theorem in the triangle MNO we get,
(NP/OP) = (MN/MO)
NP = NO + OP
= 12 + OP
(12 + OP)/OP = 10/6
6 (12 + OP) = 10 OP
72 + 6 OP = 10 OP
72 = 10 OP - 6 OP
4 OP = 72
OP = 72/4
= 18 cm
Example 2 :
In a quadrilateral ABCD, the bisectors of ∠B and ∠D intersect on AC at E. Prove that (AB/BC) = (AD/DC).
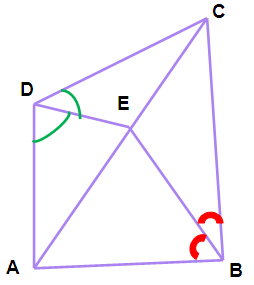
Solution :
Here DE is the internal angle bisector of angle D.
by using internal bisector theorem, we get
(AE/EC) = (AD/DC) ----- (1)
Here BE is the internal angle bisector of angle B.
(AE/EC) = (AB/BC) ----- (2)
from (1) and (2) we get,
(AB/BC) = (AD/DC)
Hence proved.
Example 3 :
The internal bisector of ∠A of triangle ABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that (BD/BE) = (CD/CE).
Solution :
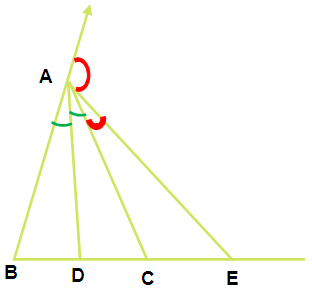
In triangle ABC, AD is the internal bisector of angle A.
by using angular bisector theorem in triangle ABC
(BD/DC) = (AB/AC) ----- (1)
In triangle ABC, AE is the internal bisector of angle A.
(BE/CE) = (AB/AC) ----- (2)
from (1) and (2) we get,
(BD/DC) = (BE/CE)
(BD/BE) = (DC/CE)
Hence proved.
Example 4 :
ABCD is a quadrilateral with AB = AD. If AE and AF are internal bisectors of ∠BAC and ∠DAC respectively,then prove that the sides EF and BD are parallel.
Solution:
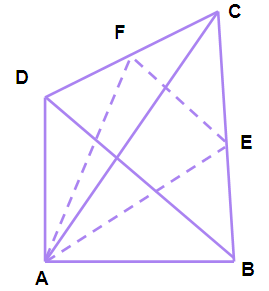
In triangle ABC, AE is the internal bisector of ∠BAC
by using bisector theorem, we get
(AB/AC) = (BE/EC) ----- (1)
In triangle ADC, AF is the internal bisector of ∠DAC
by using bisector theorem, we get
(AD/AC) = (DF/FC)
Since lengths of AD and AB are equal, we may replace AB instead of AD.
(AB/AC) = (DF/FC) ----- (2)
from (1) and (2) we get
(DF/FC) = (BE/EC)
So, EF and BD are parallel by using converse of "Thales theorem".
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

