EXAMPLE PROBLEMS OF FACTOR THEOREM IN DETERMINANTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If each element of a matrix A is a polynomial in x and if |A| vanishes for x = a, then (x - a) is a factor of | A |.
(i) This theorem is very much useful when we have to obtain the value of the determinant in ‘factors’ form.
(ii) If we substitute b for a in the determinant | A |, any two of its rows or columns become identical, then | A | = 0, and hence by factor theorem (a - b) is a factor of | A |.
(iii) If r rows (columns) are identical in a determinant of order n (n ≥ r), when we put x = a, then (x - a)r - 1 is a factor of | A |.
(iv) A square matrix (or its determinant) is said to be in cyclic symmetric form if each row is obtained from the first row by changing the variables cyclically.
(v) If the determinant is in cyclic symmetric form and if m is the difference between the degree of the product of the factors (obtained by substitution) and the degree of the product of the leading diagonal elements and if
(1) m is zero, then the required factor is a constant k
(2) m is 1, then the required factor is k(a + b + c) and
(3) m is 2, then the required factor is k(a2 + b2 + c2) + l (ab + bc + ca).
Example Problems
Solve the following problems by using Factor Theorem :
(1) Show that
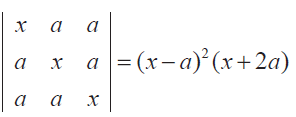
(2) Show that
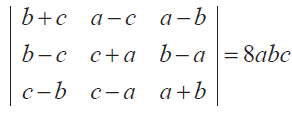
(3) Solve
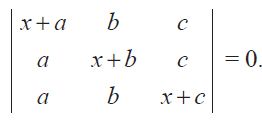
(4) Show that
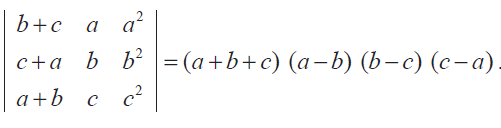
(5) Solve
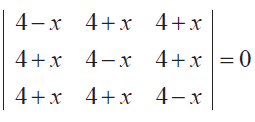
(6) Show that
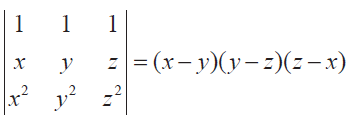
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
