FACTOR THEOREM EXAMPLES AND SOLUTIONS

About "Factor Theorem Examples and Solutions"

Factor Theorem Examples and Solutions :

Here we are going to see some example problems to understand factor theorem.

To know the steps in factor theorem, please visit the page "Solving determinants using factor theorem".

Factor Theorem Examples and Solutions - Questions

Question 1 :

Solve the following problems by using Factor Theorem :

(1) Solve

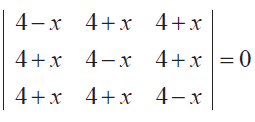
Solution :

By applying x = 0, we get identical rows and columns.

Hence the determinant will become 0.

So, x² is a factor.

By adding row 1, row 2 and row 3, we get

4 - x + 4 + x + 4 + x  =  0

12 + x = 0

x  =  -12

Hence -12 is the value which make the determinant zero. So the answers are 0, 0 and -12.

Question 2 :

Show that

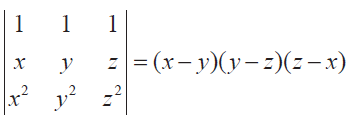
Solution :

let us apply, x = y

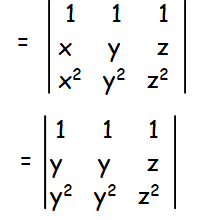
Column 1 and 2 are identical. So the determinant will become zero.

Hence (x - y) is a factor. In the same way, we may show that (y - z) and (z - x) are factors.

Sum of exponents of leading diagonal  =  3

A number of factors that we get so far  =  3

Hence the required factor is a constant (k).

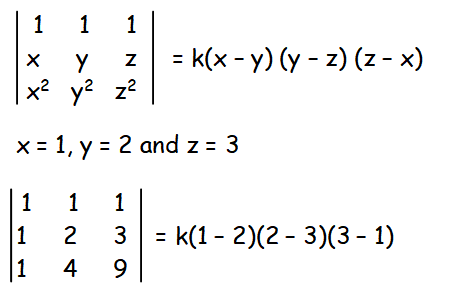
1(18 - 12) - 1(9 - 3) + 1(4 - 2)  =  k(-1)(-1)(2)

6 - 6 + 2  =  2k

k  =  1

By applying the value of k, we get the given proof.

Question 3 :

In a triangle ABC, if

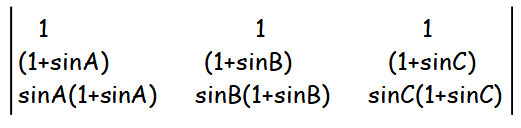
prove that triangle ABC is an isosceles triangle.

Solution :

By putting sin A = sin B, we get

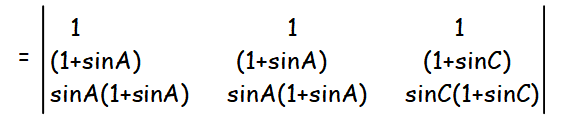
That is, by putting sin A = sin B we see that, the given equation is satisfied.

Similarly by putting sin B = sin C and sin C = sin A, the given equation is satisfied.

Thus, we have A = B or B = C or C = A.

In all cases atleast two angles are equal. Thus the triangle is isosceles.

After having gone through the stuff given above, we hope that the students would have understood, "Factor Theorem Examples and Solutions". 

Apart from the stuff given in "Factor Theorem Examples and Solutions",  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.