EULERS TEOREM ON HOMOGENOUS FUNCTION PRACTICE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In each of the following cases, determine whether the following function is homogeneous or not. If it is so, find the degree.
Problem 1 :
(i) f (x, y) = x2 y + 6x3+7 Solution
(ii)
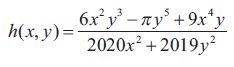
(iii)
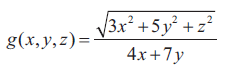
(iv)
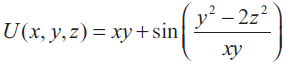
Problem 2 :
Prove that
f (x, y) = x3 − 2x2y +3xy2 + y3
is homogeneous; what is the degree? Verify Euler’s Theorem for f. Solution
Problem 3 :
Prove that
g(x, y) = x log (y/x)
is homogenous, what is the degree ? Verify Euler's theorem for g.
Problem 4 :
Prove that
g(x, y) = x log (y/x)
is homogenous, what is the degree ? Verify Euler's theorem for g.
Problem 5 :
If
v(x, y) = log [(x2+y2)/(x+y)]
prove that x(∂v/∂x) + y(∂v/∂y) = 1
Problem 6 :
If
w(x, y, z) = log[(5x3y4+7y2xz4-75y3z4)/(x2+y2)]
find x(∂w/∂x) + y(∂w/∂y) + z(∂w/∂z).

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
