DISTANCE BETWEEN TWO POINTS WORD PROBLEMS

The Pythagorean Theorem can be used to find the distance between two points in a real-world situation. We can do this by using a coordinate grid that overlays a diagram of the real-world situation.

The Pythagorean Theorem

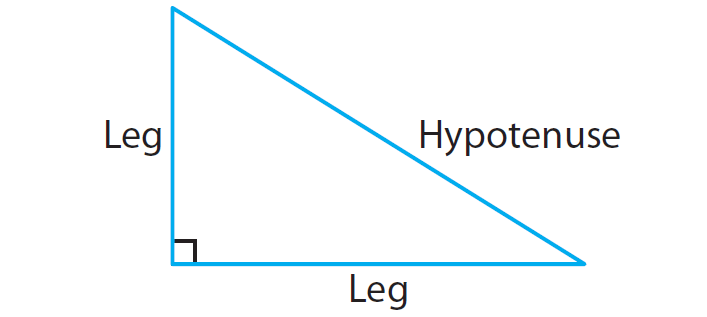
In a right triangle, the sum of the squares of the lengths of the  legs is equal to the square of the length of the hypotenuse.

If a and b are legs and c is the hypotenuse, then

a² + b²  =  c²

Problem 1 :

Gabriela wants to find the distance between her house on one side of a lake and the beach on the other side. She marks off a third point forming a right triangle, as shown in the figure. The distances in the diagram are measured in meters. Use the Pythagorean Theorem to find the straight-line distance from Gabriela’s house to the beach.

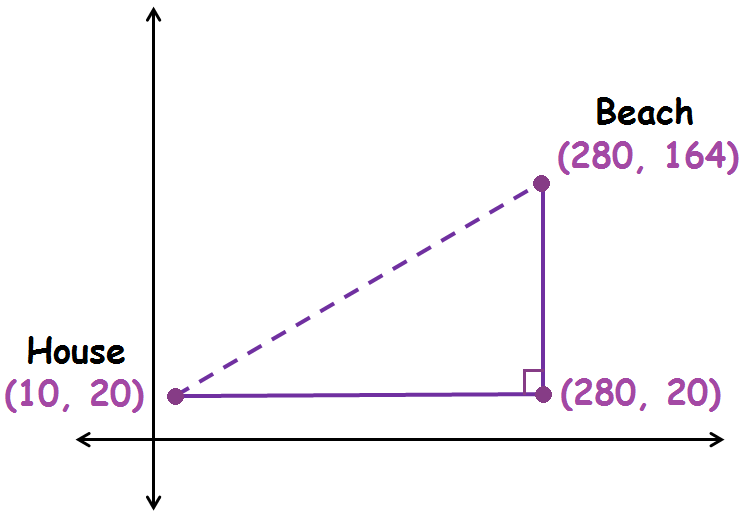
Solution :

Step 1 :

Find the length of the horizontal leg.

The length of the horizontal leg is the absolute value of the difference between the x-coordinates of the points (280, 20) and (10, 20).

|280 - 10|  =  270

The length of the horizontal leg is 270 meters.

Step 2 :

Find the length of the vertical leg.

The length of the vertical leg is the absolute value of the difference between the y-coordinates of the points (280, 164) and (280, 20).

|164 - 20|  =  144

The length of the vertical leg is 144 meters.

Step 3 :

Let a = 270, b = 144 and c represent the length of the hypotenuse. Use the Pythagorean Theorem to write the relationship between a, b and c.

a² + b²  =  c²

Step 4 :

Substitute a  =  270 and b  =  144 and solve for c. 

270² + 144²  =  c²

Simplify.

72,900 + 20,736  =  c²

93,636  =  c²

Take the square root of both sides.

√93,636  =  √c²

306  =  c

So, the distance from Jose’ house to the beach is 306 meters.

Problem 2 :

Camp Sunshine is also on the lake. Use the Pythagorean Theorem to find the distance between Gabriela’s house and Camp Sunshine to the nearest tenth of a meter.

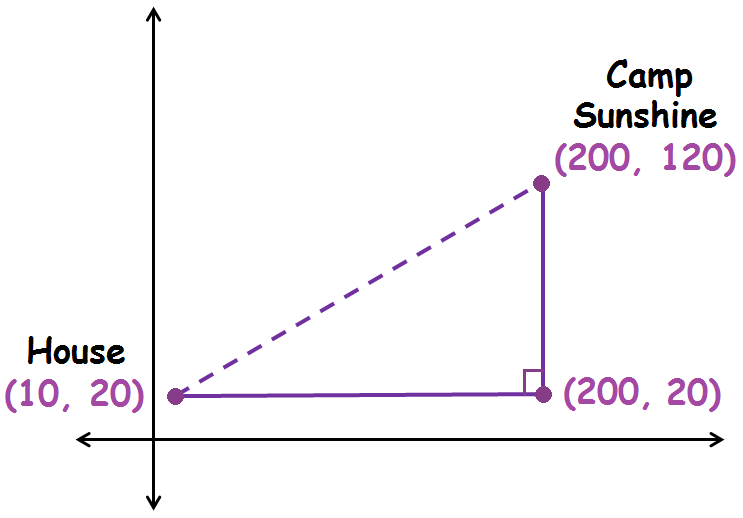
Solution :

Step 1 :

Find the length of the horizontal leg.

The length of the horizontal leg is the absolute value of the difference between the x-coordinates of the points (200, 20) and (10, 20).

|200 - 10|  =  190

The length of the horizontal leg is 190 meters.

Step 2 :

Find the length of the vertical leg.

The length of the vertical leg is the absolute value of the difference between the y-coordinates of the points (200, 120) and (200, 20).

|120 - 20|  =  100

The length of the vertical leg is 100 meters.

Step 3 :

Let a = 190, b = 100 and c represent the length of the hypotenuse. Use the Pythagorean Theorem to write the relationship between a, b and c.

a² + b²  =  c²

Step 4 :

Substitute a  =  190 and b  =  100 and solve for c. 

190² + 100²  =  c²

Simplify.

36,100 + 10,000 =  c²

46,100  =  c²

Take the square root of both sides.

√46,100  =  √c²

√46,100  =  c

Find the value of √46,100 using calculator and round to the nearest tenth

214.7  ≈  c

So, the distance from Gabriela’a house to the Camp Sunshine is about 214.7 meters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.