DETERMINING THE DOMAIN AND RANGE OF A FUNCTION

Example 1 : 

f(x) = 5x + 9

Solution : 

This is a linear function, so x and y can be any value.

Domain = {x ∊ R}

Range = {y ∊ R}

Example 2 : 

g(x) = -3(x + 1)² + 6

Solution : 

This is a quadratic equation in vertex form. The function has a maximum value at the vertex (-1, 6), x can be any value.

Domain = {x ∊ R}

Range = {y ∊ R | y ≤ 6}

Example 3 : 

h(x) = √(2 - x)

Solution : 

We cannot take the square root of a negative number, so (2 - x) must be positive or zero.

2 - x ≥ 0

x ≤ 2

Domain = {x ∊ R | x ≤ 2}

√(2 - x) means the positive square root, so y is never negative.

Range = {y ∊ R | y ≥ 0}

Example 4 : 

p(x) = 1/(x - 2)

Solution : 

The given function is a rational function. 

To find the domain of a rational function, we have to find the value of x that makes the denominator zero. 

In 1/(x - 2), if we substitute x = 2, the denominator becomes zero and it is undefined. 

So, p(x) is defined for all real values of x except x = 2. 

Domain of p(x) = R - {0}

To find range of the rational function above, find the inverse of p(x).

p(x) = 1/(x - 2)

y = 1/(x - 2)

Interchange the variables.

x = 1/(y - 2)

Solve for y in terms of x. 

(y - 2)x = 1

y - 2 = 1/x

y = 1/x + 2

y = (1 + 2x)/x

y = (2x + 1)/x

p^-1(x) = (2x + 1)/x

Find the domain of p^-1(x).

In (2x + 1)/x ,if we substitute x = 0, the denominator becomes zero and it is undefined. 

So, p^-1(x) is defined for all real values of x except x = 0. 

Domain of p^-1(x) = R - {0}

Range of p(x) = Domain of p^-1(x)

Range of p(x) = R - {0}

Example 5 : 

A gull landing on the guardrail causes a pebble to fall off the edge. The speed of the pebble as it falls to the ground is a function is v(d) = √(2gd) where d is the distance, in meters, the pebble has fallen, v(d) is the speed of the pebble, in meters per second (m/s) and g is the acceleration due to gravity—about 9.8 meters per second squared (m/s²). Determine the domain and range of v(d), the pebble’s speed.

Solution : 

d = 0 when the pebble begins to fall, and d = 346 when it lands. 

So, the domain is 0 ≤ d ≤ 346.

The pebble starts with speed 0 m/s. 

v(0) = v(d) = √(2 ⋅ 9.8 ⋅ 0) = 0

When the pebble lands, d = 346.

v(346) = √(2 ⋅ 9.8 ⋅ 346)

= √6781.6

≈ 82.4

The domain is 

{d ∊ R | 0 ≤ d ≤ 346}

and the range is

{v(d) ∊ R | 0 ≤ v(d) ≤ 82.4}

Example 6 : 

Vitaly and Sherry have 24 m of fencing to enclose a rectangular garden at the back of their house.

a) Express the area of the garden as a function of its width.

b) Determine the domain and range of the area function.

Solution : 

They need fencing on only three sides of the garden because the house forms the last side.

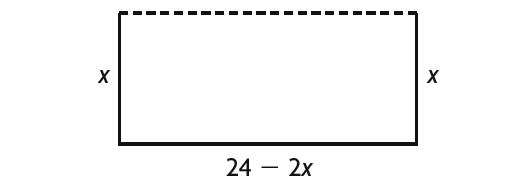
Let the width of the garden be x m.

Then the length is (24 - 2x). 

Let A(x) be the area of the garden. 

A(x) = x(24 - 2x)

= 24x - 2x²

= -2x² + 24x

= -2(x² - 12x)

= -2[x² - 2(x)(6) + 6² - 6²]

= -2[(x - 6)² - 36]

A(x) = -2(x - 6)² - 72

The smallest the width can approach is 0 m. The largest the width can approach is 12 m.

Domain = {x ∊ R | 0 < x < 12}

A(x) = -2(x - 6)² - 72 is a quadratic equation in vertex form and it has a maximum value at the vertex (6, 72).

Range = {A(x) ∊ R | 0 < A(x) ≤ 72}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.