Derivative of e to the Power Sin Square Root x
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We know the derivative of ex, which is ex.
(ex)' = ex
We can find the derivative of esin√x using chain rule.
Find ᵈʸ⁄dₓ, if
y = esin√x
Let u = √x.
y = esinu
Let v = sinu.
y = ev
Now,
y = ev ----> y is a function of v
v = sinu ----> v is is a function of u
u = √x ----> u is is a function of x
By chain rule, the derivative of y with respect to x :
Substitute y = ev, v = sinu and u = √x.
Substitute v = sinu.
Substitute u = √x.
Therefore,
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
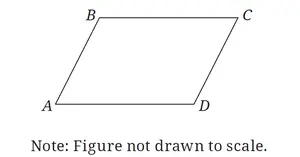
Digital SAT Math Problems and Solutions (Part - 2)
Feb 19, 26 07:14 PM
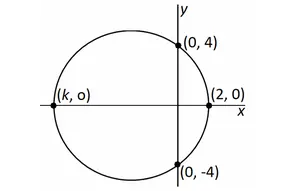
Digital SAT Math Problems and Solutions (Part - 2) -
Tricky SAT Math Problems Solved Easily
Feb 19, 26 09:11 AM
Tricky SAT Math Problems Solved Easily -
Digital SAT Math Problems and Solutions (Part - 1)
Feb 18, 26 03:01 AM
Digital SAT Math Problems and Solutions (Part - 1)