CONGRUENT TRIANGLES WORKSHEET

In each of the following problems, check whether two triangles are congruent or not.

Problem 1 :

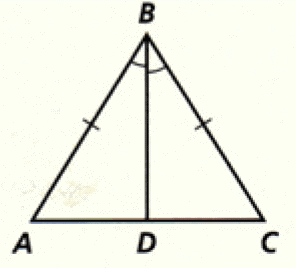
Problem 2 :

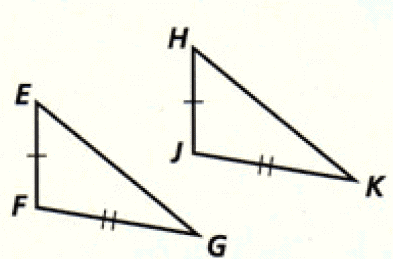
Problem 3 :

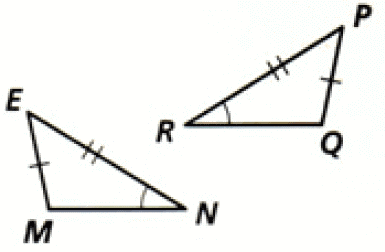
Problem 4 :

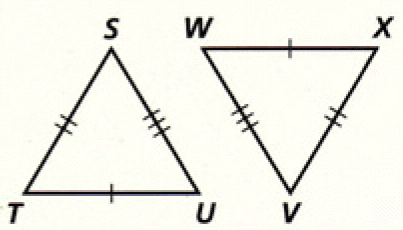
Problem 5 :

Problem 6 :

Problem 7 :

Problem 8 :

Problem 9 :

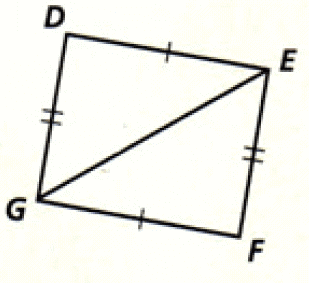
Problem 10 :

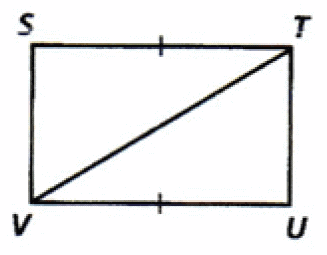
Problem 11 :

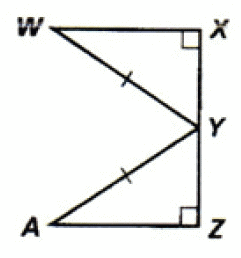
Problem 12 :

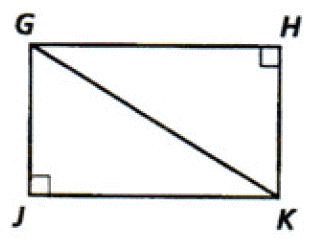
Problem 13 :

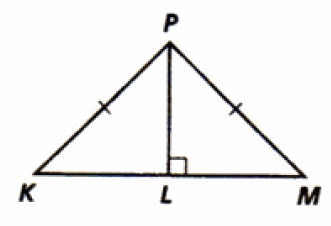
Problem 14 :

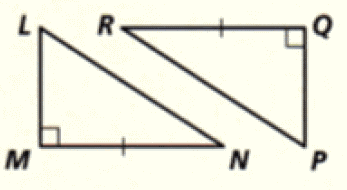
Problem 15 :

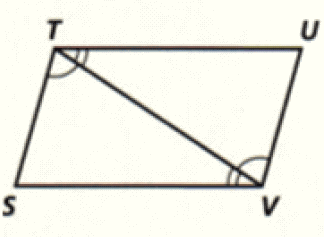
Problem 16 :

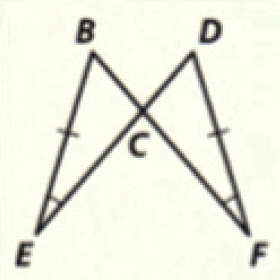
Problem 17 :

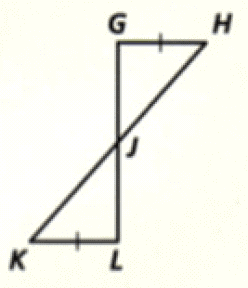
Problem 18 :

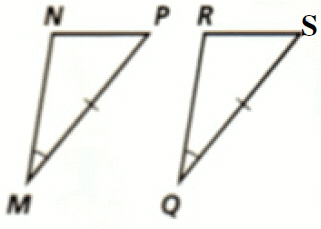
Problem 19 :

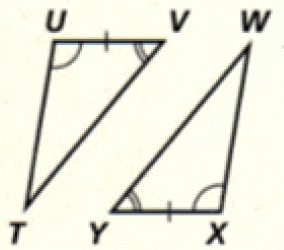
Problem 20 :

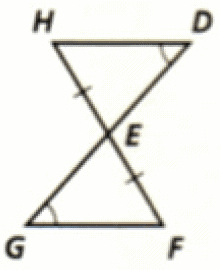
1. Answer :

(i) AD is common side for both the triangles. 

(ii) ∠ABD = ∠DBC (Given).

(iii) Sides BA and BC are congruent (Given).

Hence, the two triangles are congruent by SAS postulate.

2. Answer :

(i) Sides EF and HJ are congruent (Given).

(ii) Sides FG and JK are congruent (Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

3. Answer :

(i) ∠N = ∠R (Given). 

(ii) Sides NE and RP are congruent (Given).

(iii) Sides EM and PQ are congruent (Given).

From the above three points, we get ASS. 

But, ASS does not work for congruent triangles.

Hence, the two triangles are not congruent.

4. Answer :

(i) Sides TU and WX  are congruent (Given). 

(ii) Sides ST and XV  are congruent (Given).

(iii) Sides SU and WV  are congruent (Given).

Hence, the two triangles are congruent by SSS postulate.

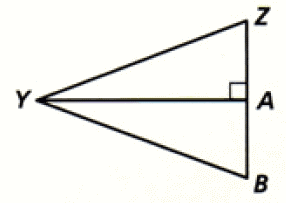
5. Answer :

(i) YA is common side for both the triangles. 

(ii) ∠YAB = ∠YAZ (Right angles).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

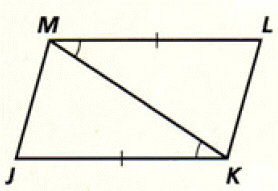
6. Answer :

(i) MK is common side of both the triangles.. 

(ii) ∠JKM = ∠KML (Given).

(iii) Sides JK and ML are congruent.

Hence, the two triangles are congruent by SAS postulate.

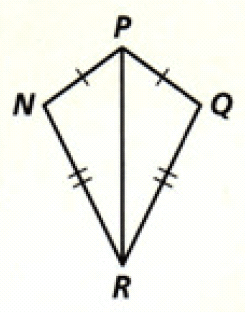
7. Answer :

(i) PR is common side for both the triangles. 

(ii) Sides PN and PQ are congruent.

(iii) Sides NR and QR are congruent.

Hence, the two triangles are congruent by SSS postulate.

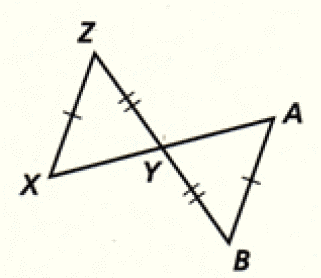
8. Answer :

(i) ∠XYZ = ∠AYB (Vertically opposite angles).

(ii) Sides YZ and YB are congruent (Given).

(iii) Sides ZX and BA are congruent (Given).

From the above three points, we get ASS.

But, ASS does not work for congruent triangles.

Hence the two triangles are not congruent.

9. Answer :

(i) GE is common side for both the triangles. 

(ii) Sides DE and GF are congruent.

(iii) Sides DG and EF are congruent.

Hence, the two triangles are congruent by SSS postulate.

10. Answer :

(i) VT is common side for both the triangles. 

(ii) Sides ST and VU are congruent (Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

11. Answer :

(i) ∠X = ∠Z (Right angles).

(ii) Sides AY and WY are congruent(Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

12. Answer :

(i) ∠J = ∠H (Right angles).

(ii) GK is common side for both the triangles.

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

13. Answer :

(i) ∠PLK = ∠PLM (Right angles).

(ii) PL is common side for both the triangles. 

(iii) Sides PK and PM are congruent (Given).

From the above three points, we get ASS.

But, ASS does not work for congruent triangles.

Hence the two triangles are not congruent.

14. Answer :

(i) ∠M = ∠Q (Given : Right angles). 

(ii) Sides MN and QR are congruent (Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

15. Answer :

(i) ∠STV = ∠UVT (Given).

(ii) TV is common side for both the triangles.

(iii) ∠SVT = ∠UTV (Given).

Hence, the two triangles are congruent by ASA postulate.

16. Answer :

(ii) ∠BCE = ∠DCE (Vertically opposite angles).

(ii) ∠E = ∠F (Given). 

(iii) Sides BE and DF are congruent.

Hence, the two triangles are congruent by AAS postulate.

17. Answer :

(i) ∠LJK = ∠HJG (Vertically opposite angles).

(ii) Sides KL and GH are congruent (Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

18. Answer :

(i) ∠M = ∠Q (Given).

(ii) Sides PM and SQ are congruent (Given).

That's all the information we can have from the given figure.

Since the information given in the figure is insufficient, we can not conclude whether the two triangles are congruent or not.

19. Answer :

(i) ∠U = ∠X (Given).

(ii) Sides UV and XY are congruent (Given).

(iii) ∠V = ∠Y (Given).

Hence, the two triangles are congruent by ASA postulate.

20. Answer :

(i) ∠G = ∠D (Given).

(ii) ∠GEF = ∠DEH (Vertically opposite angles).

(ii) Sides HE and FE are congruent (Given).

Hence, the two triangles are congruent by AAS postulate.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.