COMPOSITION OF FUNCTIONS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Using the functions f and g given below, find f o g and g o f . Check whether f o g = g o f .
Question 1 :
f(x) = x - 6, g(x) = x2 Solution
Question 2 :
f(x) = 2/x, g(x) = 2x2 - 1 Solution
Question 3 :
f(x) = (x + 6)/3, g(x) = 3 - x Solution
Question 4 :
f(x) = 3 + x, g(x) = x - 4 Solution
Question 5 :
f(x) = 4x2 - 1, g(x) = 1 + x Solution
Question 6 :
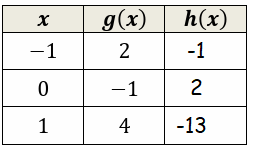
Let f(x) = 1 - 2x and h(x) = f(g(x)). Fill in the table.
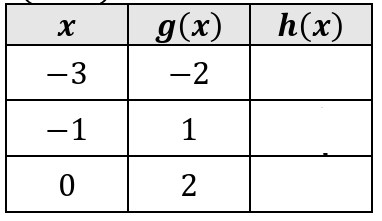
Solution
Question 7 :
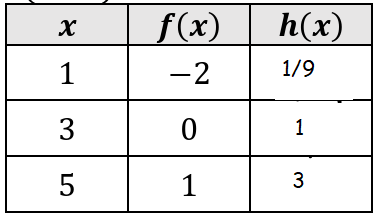
Let g(x) = 3x and h(x) = g(f(x)). Fill in the table.
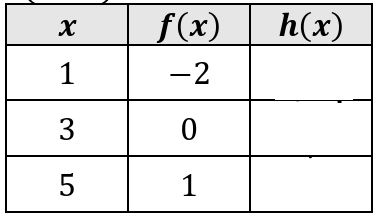
Solution
Question 8 :
Compare the quantity in column A with column B.
f(x) = 2x - 5 and g(x) = (1/2) (x + 5)
|
Column A f(2) |
Column B g(f(2)) |
[A]The quantity in Column A is greater.
[B]The quantity in Column B is greater.
[C]The two quantities are equal.
[D]The relationship cannot be determined on the basis of the information supplied.
Solution
Question 9 :
Given 𝑓(𝑥) = 5𝑥 - 2𝑏 while 𝑔(𝑥) = 4𝑏𝑥. If 𝑓[𝑔(1)] = 36, what is 𝑔(𝑓(1)) ?
Answer key
1) f o g ≠ g o f
2) f o g ≠ g o f
3) f o g ≠ g o f
4) f o g = g o f.
5) f o g ≠ g o f.
6)
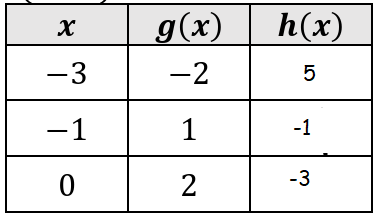
7)
8) [B]The quantity in Column B is greater is the correct answer.
9) 8
Question 1 :
f(x) = 3x + 2 and g(x) = 6x - k
Question 2 :
f(x) = 2x - k and g(x) = 4x + 5
Question 3 :
If f(x) = x2 - 3x - 1 and g(x) = 1 - x, what is the value of (f o g)(-2)
A) -3 B) -1 C) 1 D) 3
Question 4 :
If f(x) = (1 - 5x)/2 and g(x) = 2 - x, what is the value of f(g(3)) ?
A) -7 B) -2 C) 2 D) 3
Question 5 :
If f = {(-4, 12)(-2, 4) (2, 0) (3, 3/2)} and g = { (-2, 5) (0, 1) (4, -7) (5, -9) }, what is the value of (g o f) (2)
A) -9 B) -7 C) 1 D) 5
Question 6 :
The function f satisfies f(-1) = 8 and f(1) = -2. A function g(2) satisfies g(2) = 5 and g(-1) = 1, what is the value of f(g(-1))
A) -9 B) -7 C) 1 D) 5
Question 7 :
g(x) = ax2 + 24
for the function g defined above, a is constant and g(4) = 8, what is the value of g(-4) ?
a) 8 b) 0 c) -1 d) -8
Question 8 :
If f(x) = √x + 2 and g(x) = -(x - 1)2, which of the following is equivalent to g(f(a)) - 2f(a) ?
Question 9 :
The table above gives values of f and g at selected values of x. What is the value of g(f(2)) ?
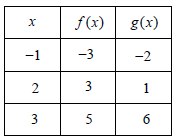
Answer Key
1) k = -5
2) k = -5/3
3) (f o g)(-2) = -1
4) f(g(3)) = 3
5) (g o f) (2) = 1
6) f(g(-1)) is 2
7) 8
8) -a - 4√a - 3
9) g(f(2)) is 6
Question 1:
Let A, B, C ⊆ N and a function f : A -> B be defined by f(x) = 2x + 1 and g : B -> C be defined by g(x) = x2 . Find the range of f o g and g o f. Solution
Question 2 :
Let f(x) = x2 - 1 . Find (i) f o f (ii) f o f o f Solution
Question 3:
If f : R -> R and g : R -> R are defined by f(x) = x5 and g(x) = x4 then check if f, g are one-one and f o g is one-one? Solution
Answer Key
1) Range of f o g {y | y = 2x2 + 1 and x ∊ N}
Range of f o g {y | y = (2x + 1)2 and x ∊ N}
2) i) f o f = x4 - 2x2
ii) (x4 - 2x2)2 - 1
3) fog is not one to one function.
Consider the functions f(x), g(x) and h(x) as given below. Find (f o g) o h and f o (g o h) in each case and also show that (f o g) o h = f o (g o h).
Question 1 :
f(x) = x - 1 , g(x) = 3x + 1 and h(x) = x2
Question 2 :
f(x) = x2, g(x) = 2x and h(x) = x + 4
Question 3 :
f(x) = x - 4, g(x) = x2 and h(x) = 3x - 5
Question 4 :
Given f(x) = -8x2, g(x) = -3x + 9 and h(x) = √x, find [(f + g)o h] (x)
Question 5 :
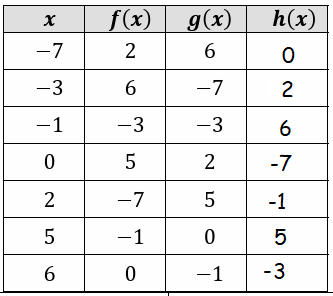
Let f(x) = 3 - x2 and h(x) = f(g(x)). Fill the table.
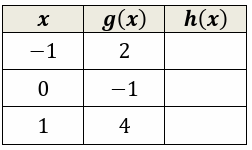
Question 6 :
Fill in the following table, given that h(x) = f(g(x))
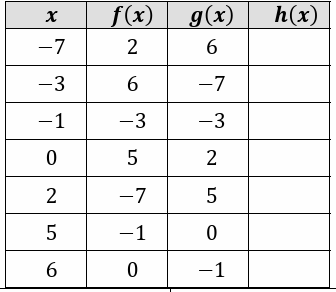
Question 7 :
Given 𝑓(𝑥) = 5𝑥 - 2𝑏 while 𝑔(𝑥) = 4𝑏𝑥. If 𝑓(𝑔(1)) = 36, what is 𝑔(𝑓(1)) ?
Answer Key
1) f o (g o h) = (f o g) o h
2) f o (g o h) = (f o g) o h
3) f o (g o h) = (f o g) o h
4) -8x - 3√x - 9
5)
6)
7) b = 2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


