COMPOSITION OF THREE FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Let A, B, C, D be four sets and let f : A--->B , g : B--->C and h : C--->D be three functions.
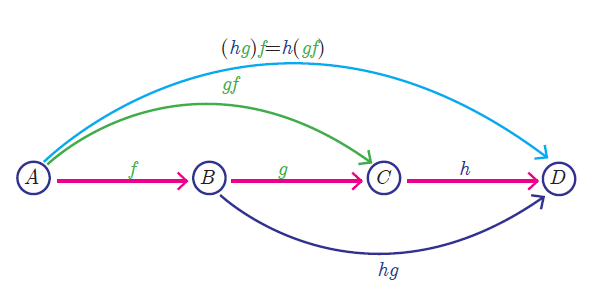
Using composite functions f o g and g o h, we get two new functions like (f o g) o h and f o (g o h).
We observed that the composition of functions is not commutative. The natural question is about the associativity of the operation.
Composition of three functions is always associative. That is,
f o (g o h) = (f o g) o h
Consider the functions f(x), g(x) and h(x) as given below. Find (f o g) o h and f o (g o h) in each case and also show that (f o g) o h = f o (g o h).
Example 1 :
f(x) = x - 1 , g(x) = 3x + 1 and h(x) = x2
Solution :
f o (g o h) :
|
g o h = g[h(x)] = g[x2] = 3x2 + 1 |
f o (g o h) = f(3x2 + 1) = 3x2 + 1 - 1 = 3x2 ----(1) |
(f o g) o h :
|
f o g = f[g(x)] = f[3x + 1] = 3x + 1 - 1 = 3x |
(f o g) o h = (f o g)[h(x)] = (f o g)(x2) = 3x2 ----(2) |
From (1) and (2),
f o (g o h) = (f o g) o h
Example 2 :
f(x) = x2, g(x) = 2x and h(x) = x + 4
Solution :
f o (g o h) :
|
g o h = g[h(x)] = g[x + 4] = 2(x + 4) = 2x + 8 |
f o (g o h) = f(2x + 8) = (2x + 8)2 = (2x)2 + 2(2x)(8) + 82 = 4x2 + 32x + 64 ----(1) |
(f o g) o h :
|
f o g = f[g(x)] = f[2x] = (2x)2 = 4x2 |
(f o g) o h = (f o g)[h(x)] = (f o g)(x + 4) = 4(x + 4)2 = 4[x2 + 2(x)(4) + 42] = 4[x2 + 8x + 16] = 4x2 + 32x + 64 ----(2) |
From (1) and (2),
f o (g o h) = (f o g) o h
Example 3 :
f(x) = x - 4, g(x) = x2 and h(x) = 3x - 5
Solution :
f o (g o h) :
|
g o h = g[h(x)] = g[3x - 5] = (3x - 5)2 |
f o (g o h) = f[(3x - 5)2] = (3x - 5)2 - 4 ----(1) |
(f o g) o h :
|
f o g = f[g(x)] = f[x2] = x2 - 4 |
(f o g) o h = (f o g)[h(x)] = (f o g)(3x - 5) = (3x - 5)2 - 4 ----(2) |
From (1) and (2),
f o (g o h) = (f o g) o h
Example 4 :
Given f(x) = -8x2, g(x) = -3x + 9 and h(x) = √x, find [(f + g)o h] (x)
Solution :
[(f + g)o h] (x) = (f + g)[h (x)]
= (f + g) (√x)
= f(√x) + g(√x)
|
f(x) = -8x2 f(√x) = -8(√x)2 = -8x |
g(x) = -3x + 9 g(√x) = -3√x + 9 = -3√x + 9 |
f(x) + g(x) = -8x + (-3√x + 9)
= -8x - 3√x - 9
Example 5 :
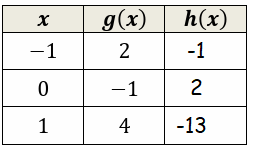
Let f(x) = 3 - x2 and h(x) = f(g(x)). Fill the table.
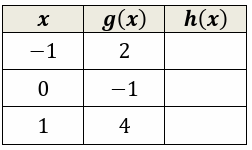
Solution :
h(x) = f(g(x))
When x = -1
h(-1) = f(g(-1))
Applying the value of g(-1), we get
= f(2)
Now using the given function f(x), let us evaluate f(2).
f(x) = 3 - x2
f(2) = 3 - 22
= 3 - 4
= -1
Then, h(-1) = f(g(-1)) = -1
When x = 0
h(0) = f(g(0))
Applying the value of g(0), we get
= f(-1)
f(x) = 3 - (-1)2
f(-1) = 3 - 1
= 2
h(0) = f(g(0)) = 2
When x = 1
h(1) = f(g(1))
Applying the value of g(1), we get
= f(4)
f(x) = 3 - 42
f(4) = 3 - 16
= -13
h(1) = f(g(1)) = -13
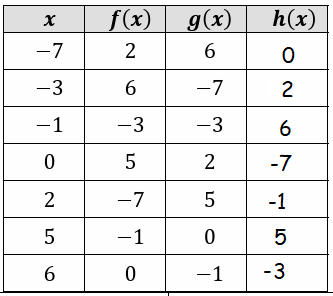
Example 6 :
Fill in the following table, given that h(x) = f(g(x))
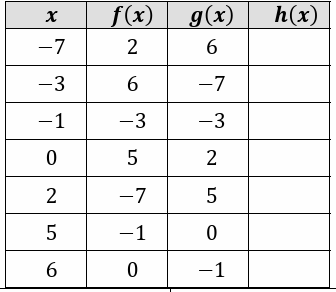
Solution :
When x = -7
h(-7) = f(g(-7))
The value g(-7) is 6.
h(-7) = f(6)
h(-7) = 0
When x = -3
h(-3) = f(g(-3))
The value g(-3) is -7.
h(-3) = f(-7)
h(-3) = 2
When x = -1
h(-1) = f(g(-1))
The value g(-1) is -3.
h(-1) = f(-3)
h(-1) = 6
When x = 0
h(0) = f(g(0))
The value g(0) is 2.
h(0) = f(2)
h(0) = -7
When x = 2
h(2) = f(g(2))
The value g(2) is 5.
h(2) = f(5)
h(2) = -1
When x = 5
h(5) = f(g(5))
The value g(5) is 0.
h(5) = f(0)
h(5) = 5
When x = 6
h(6) = f(g(6))
The value g(6) is -1.
h(6) = f(-1)
h(6) = -3
Example 7 :
Given 𝑓(𝑥) = 5𝑥 - 2𝑏 while 𝑔(𝑥) = 4𝑏𝑥. If 𝑓(𝑔(1)) = 36, what is 𝑔(𝑓(1)) ?
Solution :
Given that,
𝑓(𝑥) = 5𝑥 - 2𝑏
𝑔(𝑥) = 4𝑏𝑥.
𝑓(𝑔(1)) = 36 -----(1)
g(1) = 4b(1) ==> 4b
Applying the value of g(1) in (1), we get
𝑓(4b) = 36
Applying x = 4b as x in the function f(x).
f(4b) = 5(4b) - 2𝑏
= 20b - 2b
f(4b) = 18b
18b = 36
b = 36/18
b = 2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


