COMPOSITION OF FUNCTIONS EXAMPLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
If f(x) = 2x2 + 3 and g(x) = x + 2, find f o g.
Solution :
f o g = f[g(x)]
= f[x + 2]
= 2(x + 2)2 + 3
= 2(x2 + 4x + 4) + 3
= 2x2 + 8x + 8 + 3
= 2x2 + 8x + 11
Example 2 :
If f(x) = 5x and g(x) = x + 2, find f o g(x2).
Solution :
f o g(x2) = f[g(x2)]
= f[x2 + 2]
= 5(x2 + 2)
= 5x2 + 10
Example 3 :
If f(x) = 5x + 3 and g(x) = 7x - 2, find f o g(3).
Solution :
f o g(x) = f[g(x)]
= f[7x - 2]
= 5(7x - 2) + 3
= 35x - 10 + 3
f o g(x) = 35x - 7
f o g(3) = 35(3) - 7
= 105 - 7
= 98
Example 4 :
Using f(x) = 4x + 3 and g(x) = x - 2, find f[g(5)].
Solution :
f[g(x)] = f[x - 2]
= 4(x - 2) + 3
= 4x - 8 + 3
f[g(x)] = 4x - 5
f[g(5) = 4(5) - 5
= 20 - 5
= 15
Example 5 :
Using f(x) = 6x2 and g(x) = 14x + 4, find g o f.
Solution :
g o f = g[f(x)]
= g[6x2]
= 84x2 + 4
Example 6 :
Using f(x) = 5x + 4 and g(x) = x - 3, find g o f(6).
Solution :
g o f(x) = g[f(x)]
= g[5x + 4]
= (5x + 4) - 3
= 5x + 4 - 3
g o f(x) = 5x + 1
g o f(6) = 5(6) + 1
= 30 + 1
= 31
Example 7 :
If f(x) = x - 5 and g(x) = 2x + 3, verify f o g = g o f.
Solution :
f o g = [g(x)]
= f[2x + 3]
= (2x + 3) - 5
= 2x + 3 - 5
f o g = 2x - 2 ---->(1)
g o f = g[f(x)]
= g[x - 5]
= 2(x - 5) + 3
= 2x - 10 + 3
= 2x - 7 ---->(2)
From (1) and (2), we see that f o g ≠ g o f.
Example 8 :
Let f(x) = x + k and g(x) = 7x. If f o g(2) = 7, find k.
Solution :
f o g(2) = 7
f[g(2)] = 7
f[7(2)] = 7
f(14) = 7
14 + k = 7
k = -7
Example 9 :
Use 𝑓 and 𝑔 by the following table of values to evaluate the following
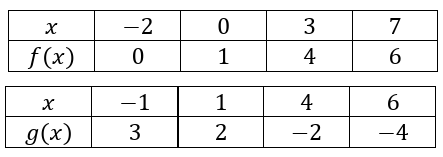
|
a) 𝑓(0) b) 𝑔(1) c) (𝑓◦𝑔)(−1) d) (𝑓◦𝑔)(4) |
e) (𝑔◦𝑓)(0) f) (𝑔◦𝑓)(7) g) (𝑓◦𝑔)(1) h) (𝑔◦𝑓)(−2) |
Solution :
a) In the first table, when x = 0, the output is 1. So,
𝑓(0) = 1
b) In the second table, when input = 1 the output is 2. So,
𝑔(1) = 2
c) (𝑓◦𝑔)(−1)
(𝑓◦𝑔)(−1) = f[g(-1)] ----(1)
Evaluating g(-1) :
g(-1) = 3
Applying the value of g(-1) in (1), we get
(𝑓◦𝑔)(−1) = f(3)
(𝑓◦𝑔)(−1) = 4
So, the value of (𝑓◦𝑔)(−1) is 4.
d) (𝑓◦𝑔)(4)
(𝑓◦𝑔)(4) = f(g(4)) ----(1)
Evaluating g(4) :
From second table, the value of g(4) is -2.
Applying the value of g(4) in (1), we get
(𝑓◦𝑔)(4) = f(-2)
Evaluating f(-2) :
f(-2) = 0
So, the value of (𝑓◦𝑔)(4) is 0.
e) (𝑔◦𝑓)(0)
(𝑔◦𝑓)(0) = g[f(0)]
Applying the value of f(0),
= g[1]
Applying the value of g(1), we get
= 2
So, the value of (𝑔◦𝑓)(0) is 2.
f) (𝑔◦𝑓)(7)
(𝑔◦𝑓)(7) = g[f(7)]
Applying the value of f(7)
= g(6)
The value of g(6) from second table, g(6) = -4
So, the value of (𝑔◦𝑓)(7) is -4.
g) (𝑓◦𝑔)(1)
(𝑓◦𝑔)(1) = f[g(1)]
Applying the value g(1) from the table.
= f[2]
The value of f(2) does not exists.
h) (𝑔◦𝑓)(−2)
(𝑔◦𝑓)(−2) = 𝑔[𝑓(−2)]
Applying the value f(-2) from table, we get f(-2) = 0
= g(0)
Finding the value of g(0), we get no result for 0 as input. Then the value of g(0) does not exists.
Example 10 :
If 𝑓 = {(3, 4),(4, 5),(5, 6),(6, 7)} and 𝑔 = {(5, 3),(6, 4),(7, −2), (8, 0)}, determine:
a) (𝑓◦𝑔)(𝑥)
b) (𝑔◦𝑓)(𝑥)
Solution :
𝑓 = {(3, 4),(4, 5),(5, 6),(6, 7)} and 𝑔 = {(5, 3),(6, 4),(7, −2), (8, 0)}
a) (𝑓◦𝑔)(𝑥)
For the function g, the inputs are 5, 6, 7 and 8
When x = 5
(𝑓◦𝑔)(𝑥) = (𝑓◦𝑔)(5)
= f[g(5)] -----(1)
From the relation g :
g(5) = 3
= f(3)
The value of f(3) is 4. Then the answer for (𝑓◦𝑔)(5) is 4.
When x = 6
(𝑓◦𝑔)(𝑥) = (𝑓◦𝑔)(6)
= f[g(6)] -----(1)
From the relation g :
g(6) = 4
= f(4)
The value of f(4) is 5. Then the answer for (𝑓◦𝑔)(6) is 5.
When x = 7
(𝑓◦𝑔)(𝑥) = (𝑓◦𝑔)(7)
= f[g(7)] -----(1)
From the relation g :
g(7) = -2
= f(-2)
The value of f(-2) is none. Then the answer for (𝑓◦𝑔)(7) does not exists.
When x = 8
(𝑓◦𝑔)(𝑥) = (𝑓◦𝑔)(8)
= f[g(8)] -----(1)
From the relation g :
g(8) = 0
= f(0)
The value of f(0) is none. Then the answer for (𝑓◦𝑔)(8) does not exists.
b) (𝑔◦𝑓)(𝑥)
(𝑔◦𝑓)(𝑥) = g[f(x)]
𝑓 = {(3, 4),(4, 5),(5, 6),(6, 7)} and 𝑔 = {(5, 3),(6, 4),(7, −2), (8, 0)}
For the function f, the inputs are 3, 4, 5 and 6.
|
When x = 3 (𝑔◦𝑓)(3) = g[f(3)] = g(4) (𝑔◦𝑓)(3) = does not exists |
When x = 4 (𝑔◦𝑓)(4) = g[f(4)] = g(5) (𝑔◦𝑓)(4) = 3 |
|
When x = 5 (𝑔◦𝑓)(5) = g[f(5)] = g(6) (𝑔◦𝑓)(5) = 4 |
When x = 6 (𝑔◦𝑓)(6) = g[f(6)] = g(7) (𝑔◦𝑓)(6) = -2 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

