COMPARING DIFFERENCES IN CENTERS TO VARIABILITY
About "Comparing differences in centers to variability"
Comparing differences in centers to variability :
Recall that to find the mean absolute deviation (MAD) of a data set, first find the mean of the data. Next, take the absolute value of the difference between the mean and each data point. Finally, find the mean of those absolute values.
Comparing differences in centers to variability - Example
The tables show the number of minutes per day students in a class spend exercising and playing video games. What is the difference of the means as a multiple of the mean absolute deviations ?
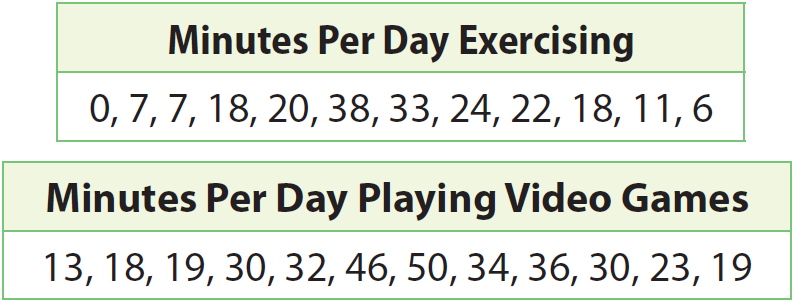
Solution :
Step 1 :
Calculate the mean number of minutes per day exercising.
0 + 7 + 7 + 18 + 20 + 38 + 33 + 24 + 22 + 18 + 11 + 6 = 204
Divide the sum by the number of students.
204 ÷ 12 = 17
Step 2 :
Calculate the mean absolute deviation for the number of minutes exercising.
|
|0-17| = 17 |7-17| = 10 |7-17| = 10 |18-17| = 1 |20-17| = 3 |38-17| = 21 |
|33-17| = 16 |24-17| = 7 |22-17| = 5 |18-17| = 1 |11-17| = 6 |6-17| = 11 |
Find the mean of the absolute values.
17 + 10 + 10 + 1 + 3 + 21+ 16 + 7 + 5 + 1 + 6 + 11 = 108
Divide the sum by the number of students.
108 ÷ 12 = 9
Step 3 :
Calculate the mean number of minutes per day playing video games. Round to the nearest tenth.
13+18+19+30+32+46+50+34+36+30+23+19 = 350
Divide the sum by the number of students.
350 ÷ 12 ≈ 29.2
Step 4 :
Calculate the mean absolute deviation for the numbers of minutes playing video games.
|
|13-29.2| = 16.2 |18-29.2| = 11.2 |19-29.2| = 10.2 |30-29.2| = 0.8 |32-29.2| = 2.8 |46-29.2| = 16.8 |
|50-29.2| = 20.8 |34-29.2| = 4.8 |36-29.2| = 6.8 |30-29.2| = 0.8 |23-29.2| = 6.2 |19-29.2| = 10.2 |
Find the mean of the absolute values. Round to the nearest tenth.
16.2 + 11.2 + 10.2 + 0.8 + 2.8 + 16.8 + 20.8 + 4.8 + 6.8 + 0.8 + 6.2 + 10.2 = 107.6
Divide the sum by the number of students.
107.6 ÷ 12 ≈ 9
Step 5 :
Find the difference in the means.
Subtract the lesser mean from the greater mean.
29.2 - 17 = 12.2
Step 6 :
Write the difference of the means as a multiple of the mean absolute deviations, which are similar but not identical.
Divide the difference of the means by the MAD.
12.2 ÷ 9 ≈ 1.36
The means of the two data sets differ by about 1.4 times the variability of the two data sets.
Comparing differences in centers to variability - Practice question
Question :
The high jumps in inches of the students on two intramural track and field teams are shown below. What is the difference of the means as a multiple of the mean absolute deviations ?
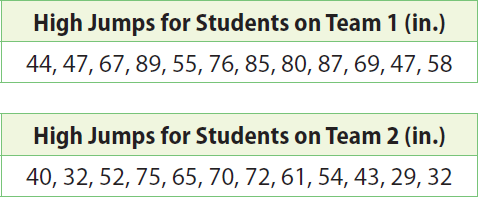
Solution :
About 1.1 times the MAD.
After having gone through the stuff given above, we hope that the students would have understood "Comparing differences in centers to variability".
Apart from the stuff given above, if you want to know more about "Comparing differences in centers to variability", please click here
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
