TYPES OF ANGLES

In geometry, angles can be classified according to the size. There are six different types of angles.

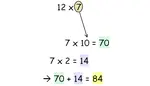
Acute Angle

An angle that is greater than 0° and less than 90° is called acute angle.

Example :

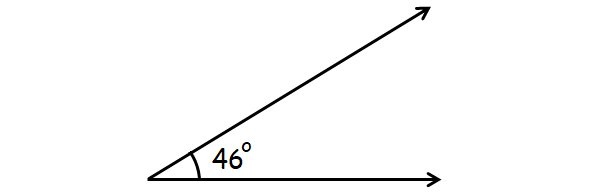
Right Angle

An angle that is exactly 90° is called right  angle.

Example :

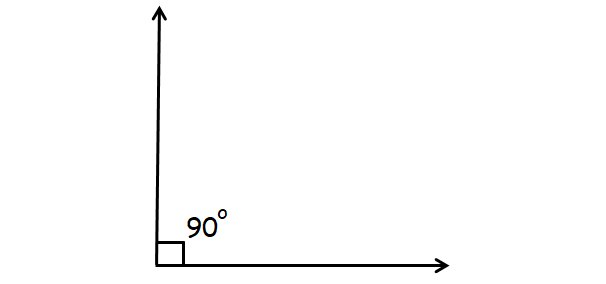
Obtuse Angle

An angle that is greater than 90° and less than 180° is called obtuse angle.

Example :

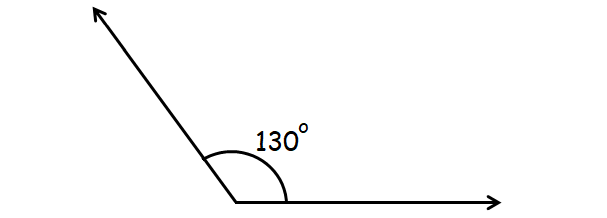
Straight Angle

An angle that is exactly 180° is called straight angle.

Example :

Reflex Angle

An angle that is greater than 180° and less than 360° is called reflex angle.

Example :

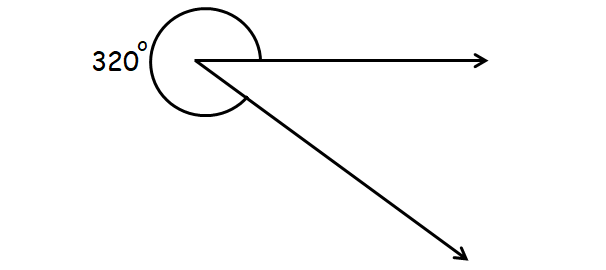
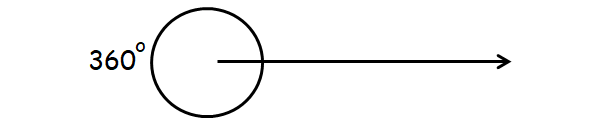
Full Angle

An angle that is exactly 360° is called full angle.

Example :

Classifying angles as acute, right, obtuse straight, reflex or full angle :

1) 35° ----> Acute angle

2) 85° ----> Acute angle

3) 95° ----> Obtuse angle

4) 135° ----> Obtuse angle

5) 205° ----> Reflex angle

6) 180° ----> Straight angle

7) 90° ----> Right angle

8) 360° ----> Full angle

9) 15° ----> Acute angle

10) 270° ----> Reflex angle

Word Problems on Types of Angles

Problem 1 :

If 4 times the sum of an angle and 5 is 32, find the type of the angle.

Solution :

Let x be the required angle.

4(x + 5) = 32

4x + 20 = 32

4x = 12

x = 3

Angle = 3°

Since 3° is less than 90°, the type of the angle is acute angle.

Problem 2 :

If 2 times the sum of 3 times of an angle and 20 is 1024, find the type of the angle.

Solution :

2(3x + 20) = 1024

3x + 20 = 512

3x = 498

x = 166

Angle = 166°

Since 166° is greater than 90° but less than 180°, the type of the angle is obtuse angle.

Problem 3 :

If the sum of 5 times of an angle and 2 is 1222, find the type of the angle.

Solution :

5x + 2 = 1222

5x = 1220

x = 244

Angle = 244°

Since 244° is greater than 180° but less than 360°, the type of the angle is reflex angle.

Problem 4 :

If the sum of 5 times of an angle and 2 is 1222, find the type of the angle.

Solution :

5(x - 2) = 440

x - 2 = 88

x = 90

Angle = 90°

Since the angle is exactly 90°, the type of the angle is right angle.

Problem 5 :

If 7 times the difference between 3 times of an angle and 5 is 3745, find the type of the angle.

Solution :

7(3x - 5) = 3745

3x - 5 = 535

3x = 540

x = 180

Angle = 180°

Since the angle is exactly 180°, the type of the angle is straight angle.

Problem 6 :

If 2 times the difference between 9 times of angle and 15 is 6450,  find the type of the angle.

Solution :

2(9x - 15) = 6450

9x - 15 = 3225

9x = 3240

x = 360

Angle = 360°

Since the angle is exactly 360°, the type of the angle is full angle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.