CHECK IF THE LINEAR IS A FACTOR OF THE GIVEN POLYNOMIAL

Problem 1 :

Determine whether (x+1) is a factor of the following polynomials.

(i)  6x⁴+7x³-5x-4

(ii)  2x⁴+9x³+2x²+10x+15

(iii)  3x³+8x²-6x-5

(iv)  x³-14x²+3x+12

(i)  Solution :

6x⁴+7x³-5x-4

By factor theorem, if p(-1)  =  0, then (x+1) is a factor of

p(x) =  6x⁴+7x³-5x-4

p(-1)  = 6(-1)⁴+7(-1)³-5(-1)-4

=  6-7+5-4

p(-1)  =  0

(x+1) is a factor of the given polynomial.

(ii)  Solution :

2x⁴+9x³+2x²+10x+15

By factor theorem, if p(-1) = 0, then (x+1) is a factor of 

p(x)  =  2x⁴+9x³+2x²+10x+15

p(-1)  =  2(-1)⁴+9(-1)³+2(-1)²+10(-1)+15

=  2-9+2-10+15

=  0

So, (x+1) is a factor of the given polynomial.

(iii)  Solution :

3x³+8x²-6x-5

By factor theorem, if p(-1) = 0, then (x+1) is a factor of 

p(x)  =  3x³+8x²-6x-5

p(-1)  =  3(-1)³+8(-1)²-6(-1)-5

=  -3+8+6-5

p(-1)   ≠  0

(x+1) ix not the factor of 3x³+8x²-6x-5.

(iv)  Solution :

x³-14x²+3x+12

By factor theorem, if p(-1) = 0, then (x+1) is a factor of

p(x)  =  x³-14x²+3x+12

p(-1)  =  (-1)³-14(-1)²+3(-1)+12

p(-1)  =  -1-14-3+12

p(-1)  ≠  0

(x+1) is not the factor of x³-14x²+3x+12.

Problem 2 :

Determine whether (x+4) is a factor of

x³ + 3x² - 5x + 36

Solution :

By factor theorem, if p(-4) = 0, then (x+4) is a factor of

p(x)  =  x³ + 3x² - 5x + 36

p(-4)  =  (-4)³+3(-4)²-5(-4)+36

=  -64+48+20+36

p(-4)  ≠  0

(x+4) is not the factor of x³+3x²-5x+36.

Problem 3 :

Using factor theorem show that (x-1) is a factor of  

4x³-6x²+9x-7

Solution :

By factor theorem, if p(1) = 0, then (x-1) is a factor of 

p(x)  =  4x³-6x²+9x-7

p(1)  =  4(1)³-6(1)²+9(1)-7

=  4-6+9-7

p(1)  =  0

(x-1) is the factor of 4x³-6x²+9x-7.

Problem 4 :

Determine whether (2x+1) is a factor of

4x³+4x²-x-1

Solution :

By factor theorem, if p(-1/2) = 0, then (2x+1) is a

Factor of p(x)  =  4x³+4x²-x-1

p(-1/2)  =  4(-1/2)³+4(-1/2)²-(-1/2)-1

=  -1/2+1+1/2-1

p(-1/2)  =  0

(2x+1) is the factor of 4x³+4x²-x-1.

Problem 5 :

Determine the value of p if (x+3) is a factor of

x³-3x²-px+24

Solution :

By factor theorem, if p(-3) = 0, then (x+3) is a 

factor of p(x)  =  x³-3x²-px+24

p(-3)  =  (-3)³-3(-3)²- p(-3)+24

This implies that  -27-27+3p+24  =  0

-30 + 3p  =  0

3p  =  30

p  =  10

So, the value of p is 10.

Problem 6 :

g(x) = ax² + 24

For the function g defined above, a is constant and g(4) = 8. What is the value of g(-4) ?

a)  8     b)  0     c)  -1     d)  -8

Solution :

g(x) = ax² + 24

g(4) = 8

When x = 4, we get

g(4) = a(4)² + 24

8 = 16a + 24

8 - 24 = 16a

16a = -16

a = -16/16

a = -1

Applying the value of a, we get

g(x) = -1x² + 24

To find the value of g(-4), we apply -4 in the place of x.

g(-4) = -1(-4)² + 24

= -1(16) + 24

= -16 +  24

= 8

So, the answer is 8, option a is correct.

Problem 7 :

If x² + x - 12 divides p(x) = x³ + ax² + bx - 84 exactly find a and b.

Solution :

By solving the equation x² + x - 12 = 0, we get

x² + x - 12 = 0

(x + 4) (x - 3) = 0

x + 4 and x - 3 are factors. Equating each factor to 0, we get

x = -4 and x = 3

Here -4 and 3 are solutions.

Since -4 and 3 are solutions, p(-4) and p(3) the remainder will be 0.

p(x) = x³ + ax² + bx - 84

p(-4) = (-4)³ + a(-4)² + b(-4) - 84

0 = -64 + 16a - 4b - 84

0 = -148 + 16a - 4b

148 = 16a - 4b

Dividing by 4, we get

4a - b = 37 ------(1)

p(3) = (3)³ + a(3)² + b(3) - 84

0 = 27 + 9a + 3b - 84

0 = -57 + 9a + 3b

57 = 9a + 3b

Dividing by 3, we get

19 = 3a + b

3a + b = 19 -------(2)

(1) + (2)

4a - b + 3a + b = 37 + 19

7a = 56

a = 8

Applying the value of a in (1), we get

4(8) - b = 37

32 - b = 37

b = 32 - 37

b = -5

Problem 8 :

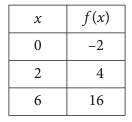
Some values of the linear function f are shown in the table above, what is the value of f(3) ?

a)  6   b)  7    c)  8     d)  9

Solution :

The table shows the linear function, every linear function will be in the form of 

y = mx + b

(0, -2) and (2, 4)

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

= (4 + 2) / (2 - 0)

= 6 / 2

m = 3

y = 3x + b

Applying one of the points from the table (0, -2), we get

-2 = 3(0) + b

b = -2

f(x) = y = 3x - 2

To find f(3), we get

f(3) = 3(3) - 2

= 9 - 2

= 7

So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.