WHEN TO USE CHAIN RULE

If

y  =  f(u) and u  =  g(x)

and both dy/du and du/dx exists, then the derivative of the function

y  =  f[g(x)] exists and is given by 

dy/dx  =  (dy/du) ⋅ (du/dx)

Example 1 :

Differentiate log √x

Solution :

Let y  =  log √x

Using chain rule :

y  =  log √x

dy/dx  =  (1/√x)⋅(1/2√x)

dy/dx  =  1/2x  ---(1)

Using substitution  :

y  =  log √x

Let t  =  √x, then y  =  log t

dy/dx  =  (dy/dt)⋅(dt/dx)

dy/dt  =  1/t and dt/dx  =  1/2√x

=  (1/t)⋅(1/2√x)

By replacing t by √x, we get

=  (1/√x)⋅(1/2√x)

dy/dx  =  1/2x  ---(2)

Note :

In both ways, we should get the same answer.

Example 2 :

Differentiate log sin (x²+2x+3)

Solution :

Let y  =  log sin (x²+2x+3)

dy/dx  =  (1/sin (x²+2x+3)) cos (x²+2x+3)(2x+2)

  =  2(x+1)cos (x²+2x+3)/sin (x²+2x+3)

dy/dx  =  2(x+1) cot (x²+2x+3)

Example 3 :

Differentiate [e^-6t + sin(2-t)]³

Solution :

Let y  =  [e^-6t + sin(2-t)]³

dy/dx  =  3[e^-6t + sin(2-t)]²[e^-6t (-6) + cos(2-t) (-1)]

=  3[e^-6t + sin(2-t)]²[-6e^-6t - cos(2-t)]

dy/dx  =  -3[e^-6t + sin(2-t)]²[6e^-6t + cos(2-t)]

Example 4 :

Differentiate ((ln(x²+1) + tan^-1(6x))¹⁰

Solution :

Let y  =  ((ln(x²+1) + tan^-1(6x))¹⁰

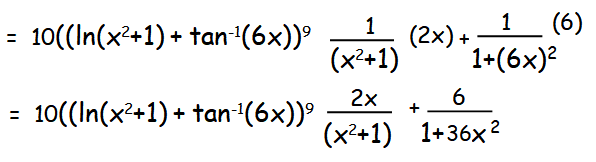
Example 5 :

Differentiate √(5x+ tan(4x))

Solution :

Let y  =  √(5x+ tan(4x))

dy/dx  =  [1/2√(5x+ tan(4x))] [5+sec²(4x) 4]

dy/dx  =  [1/2√(5x+ tan(4x))] [5+4sec²(4x)]

Example 6 :

Differentiate cos(x²e^x)

Solution :

y  =  cos(x²e^x)

dy/dx  =  -sin(x²e^x) [x² e^x + e^x 2x]

dy/dx  =  -xe^x(x + 2)sin(x²e^x) 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.