AREA OF DIFFERENT TYPES OF TRIANGLES
Finding area of a triangle is depending on the type of it.
To know the different types of triangles,
General Formula for Area of Triangle :
= (1/2) ⋅ base ⋅ height
Formula for Area of Scalene Triangle :
= √[s(s - a)(s - b)(s - c)]
where
S = (a + b + c) / 2
Here a, b and c are side lengths of the triangle.
Formula for Area of Equilateral Triangle :
= (√3/4)a2
Practice Problems
Problem 1 :
Find the area of the equilateral triangle having the side length 10 cm.
Solution :
Formula for area of equilateral triangle is
= (√3/4) a2
Substitute 10 for a.
= (√3/4) (10)2
= (√3/4) x (10) x (10)
= (√3) x (5) x (5)
= 25 √3 cm2
So, area of the given equilateral triangle is 25 √3 square cm.
Problem 2 :
The altitude drawn to the base of an isosceles triangles is 8 cm and the perimeter is 32 cm. Find the area of the triangle.
Solution :
Let ABC be the isosceles triangle and AD be the altitude as shown below.
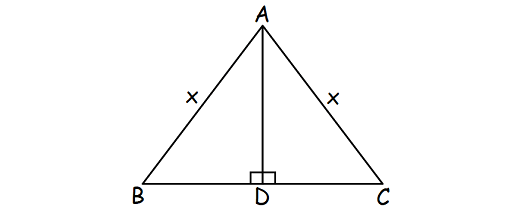
Because the triangle is isosceles, the length of two sides will be equal and the altitude bisects the base of the triangle.
Let AB = AC = x cm.
Perimeter of triangle ABC = 32 cm
AB + BC + CA = 32
x + BC + x = 32
BC = 32 - 2x -----(1)
DC = BC/2
DC = (32 - 2x) / 2
DC = 16 - x
In right triangle ADC,
AC2 = AD2 + DC2
x2 = 82 + (16 - x)2
x2 = 64 + 162 + x2 - 32x
32x = 64 + 256
32x = 320
x = 10 cm
Then,
(1)-----> BC = 32 - 2(10)
BC = 32 - 20
BC = 12 cm
Area of triangle ABC = (1/2) x (bh)
= (1/2) x (12 x 8)
= 48 square cm
Problem 3 :
Find the area of the scalene triangle whose side lengths are 12 cm, 18 cm and 20 cm.
Solution :
Because the lengths of the three sides are different, the triangle is scalene triangle.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √[s(s - a)(s - b)(s - c)]
Substitute.
= √[25 x (25 - 12) x (25 - 18) x (25 - 20)]
= √(25 x 13 x 7 x 5)
= 5√455
So, area of the given scalene triangle is 5 √455 square cm.
Problem 4 :
The sides of a triangle are 12 cm, 16 cm and 20 cm. Find the altitude to the longest side.
Solution :
In order to find the altitude to the longest side of a triangle, first we have to find the area of the triangle.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √[s(s - a)(s - b)(s - c)]
Substitute.
= √[24 x (24 - 12) x (24 - 16) x (24 - 20)]
= √(24 x 12 x 8 x 4)
= 96 cm2
Because we want to find the altitude to the longest side, the longest side will be the base of the triangle as shown below.
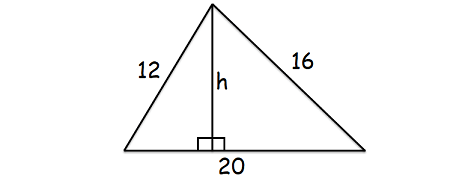
Here, the longest side is 20 cm.
Area of the above triangle = 96 cm2
(1/2) x 20 x h = 96
10h = 96
Divide each side by 10.
h = 9.6 cm
So, the altitude to the longest side is 9.6 cm.
Problem 5 :
Area of a triangle is 1176 cm2. If its base and corresponding altitude are in the ratio 3 : 4, then find the the altitude of the triangle.
Solution :
From the given information,
base of the triangle = 3x
altitude = 4x
area of the triangle = 1176
(1/2) x (3x) x (4x) = 1176
6x2 = 1176
Divide each side by 6.
x2 = 196
x = 14
Then,
altitude of the triangle = 4x = 4(14) = 56 cm
Problem 6 :
The sides of a triangle are in the ratio (1/2) : (1/3) : (1/4). If the perimeter is 52 cm, then find the length of the smallest side.
Solution :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length of smallest side is 12 cm.
Problem 7 :
The area of the triangle is 216 cm2 and the sides are in the ratio 3 : 4 : 5. Find the perimeter of the triangle.
Solution :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√[s(s - a)(s - b)(s - c)] = 216
√[6x(6x - 3x)(6x - 4x)(6x - 5x)] = 216
√[6x(3x)(2x(x] = 216
√(36x4) = 216
6x2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
Perimeter of the triangle is
= 18 + 24 + 30
= 72 cm
Problem 8 :
One side of a right angle triangle is twice the other,and the hypotenuse is 10 cm. Find the area of the triangle.
Solution :
Let 'x' be the length of one of the legs of the triangle.
Then, the length of the other leg is 2x.
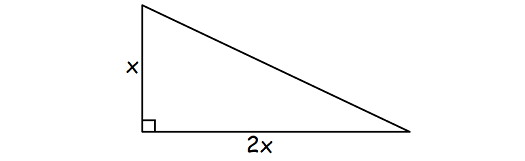
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4x2 = 100
5x2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of triangle is
= (1/2)(x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2
Problem 9 :
If the perimeter of the isosceles right triangle is (6 + 3√2) cm, then find the area of the triangle.
Solution :
Because the given triangle is isosceles right triangle, the length of two sides will be equal.
Let 'x' be the length of one of the two equal sides and 'y' be the length of the hypotenuse.
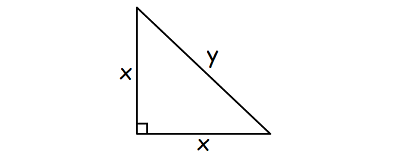
Using Pythagorean theorem,
y2 = x2 + x2
y2 = 2x2
√y2 = √(2x2)
y = √2x -----(1)
Perimeter of the triangle = 6 + 3√2
x + x + y = 6 + 3√2
2x + y = 6 + 3√2
Substitute √2x for y.
2x + √2x = 6 + 3√2
x(2 + √2) = 3(2 + √2)
x = 3
Area of triangle is
= (1/2)(x) (x)
= (1/2)(3)(3)
= 4.5 cm2
Problem 10 :
If the area of the equilateral triangle is 24√3 square cm, then find its perimeter.
Solution :
Area of equilateral triangle = 24√3 cm2
(√3/4) a2 = 24√3
a2/4 = 24
a2 = 96
√a2 = √96
a = √(16 x 6)
a = 4√6
Formula for perimeter of an equilateral triangle is
= 3a
Substitute 4√6 for a.
= 3(4√6)
= 12√6 cm
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Point Symmetry Worksheet
Jun 05, 20 07:45 PM
Point Symmetry Worksheet
-
Point Symmetry
Jun 05, 20 07:34 PM
Point Symmetry - Concept - Example - Problems with step by step explanation
-
Symmetry
Jun 05, 20 07:18 PM
Symmetry - Concept - Examples
