TYPES OF TRIANGLES

Triangles can be broadly classified into two types.

1. Triangles based on the lengths of their sides.

2. Triangle based on their angles.

Equilateral Triangle

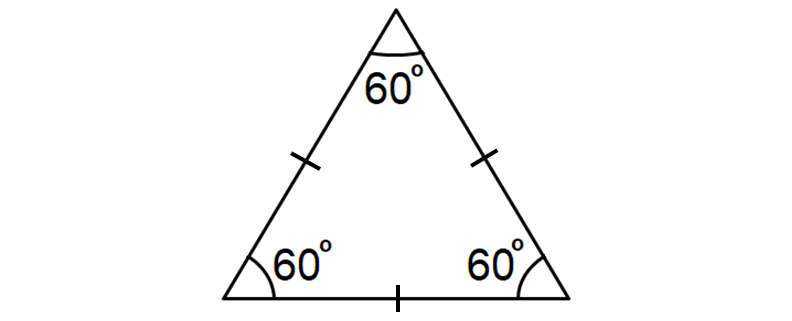
An equilateral triangle is a triangle in which all the three sides will be equal.

Each angle will be 60°.

Isosceles Triangle

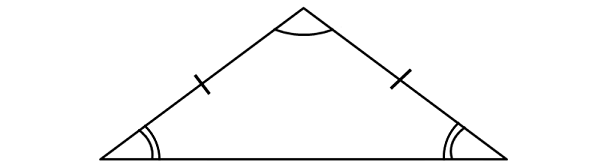
A triangle with two equal sides is called as isosceles triangle. The angles corresponding to the equal sides will always be equal.

Scalene Triangle

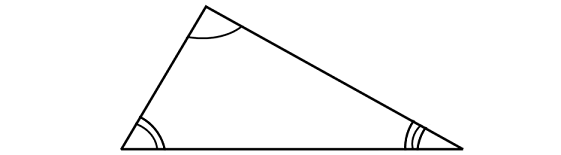
In a scalene triangle the length of all the three sides will be different. And also all the three angles will be different.

Acute Triangle

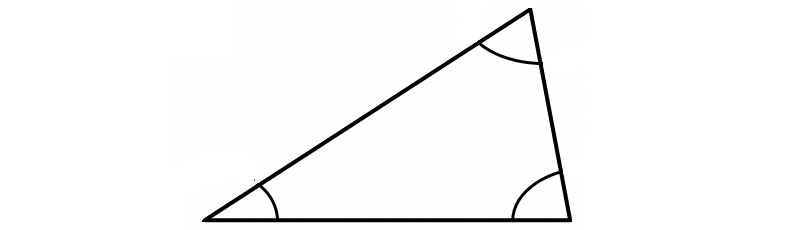
An acute triangle is a triangle with all three angles are less than 90°.

Right Triangle

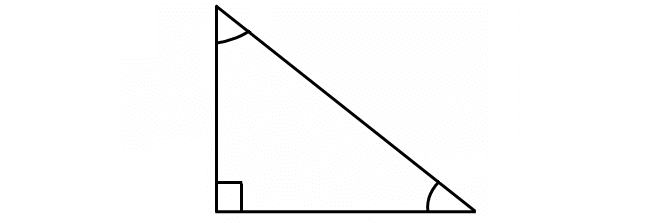
A right triangle is the triangle in which one of the angles is 90°.

Obtuse Triangle

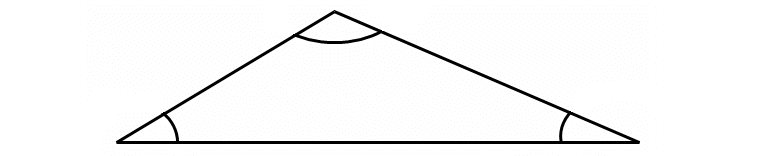
An obtuse triangle is a triangle in which one of the angles is obtuse (greater than 90°).

Solved Problems

Problem 1 :

Identify the type of triangle whose angles are 35°, 40°, 105°.

Solution :

(i) All the given three angles are different

(ii) One of the angles is greater than 90°

So, the given triangle is a scalene and obtuse triangle.

Problem 2 :

Identify the type of triangle whose angles are 55°, 65°, 60°.

Solution :

(i) All the given three angles are different

(ii) All the three angles are less than 90°

So, the given triangle is a scalene and acute triangle.

Problem 3 :

Identify the type of triangle whose angles are 50°, 40°, 90°.

Solution :

(i) All the given three angles are different

(ii) One of the angles is 90°

So, the given triangle is a scalene and right triangle.

Problem 4 :

Identify the type of triangle whose angles are 45°, 45°, 90°.

Solution :

(i) Two of the given angles are equal

(ii) One of the angles is 90°

So, the given triangle is an isosceles and right triangle.

Problem 5 :

Identify the type of triangle whose angles are 70°, 70°, 40°.

Solution :

(i) Two of the given angles are equal

(ii) All the three angles are less than 90°

So, the given triangle is an isosceles and acute triangle.

Problem 6 :

Identify the type of triangle whose angles are 30°, 30°, and 120°.

Solution :

(i) Two of the given angles are equal

(ii) One of the angles is greater than 90°

So, the given triangle is an isosceles and obtuse triangle.

Problem 7 :

Identify the type of triangle whose sides are 5 cm, 6 cm and 7 cm.

Solution :

The length of all the three sides are different.

So, the given triangle is a scalene triangle.

Problem 8 :

Identify the type of triangle whose sides are 6 cm, 6 cm and 8 cm.

Solution :

The lengths of two of the sides are equal.

So, the given triangle is an isosceles triangle.

Problem 9 :

If (3x + 3)° is one of the angles of an acute triangle, then find the value of x.

Solution :

Since the given triangle is acute triangle, all the three angles will be less than 90°.

So, (3x + 3)° will also be less than 90°.

(3x + 3)° < 90

3x < 87

x < 29

Problem 10:

If 50°, 40° and (2x + 4)°are the angles of a right triangle, then find the value of x.

Solution :

Since the given triangle is a right triangle, one of the angles must be 90°.

In the given three angles 50°, 40° and (2x+4)°, the first two angles are not right angles.

So the third angle (2x + 4)° must be right angle.

(2x + 4)° = 90°

2x + 4 = 90

2x = 86

x = 43

Problem 11 : 

The sides of a triangle are 6cm, 8cm and 10cm. Check whether it is a right triangle.

Solution : 

6² = 36, 8² = 64, 10² = 100

36 + 64 = 100

6² + 8² = 10²

Sum of squares of two sides is equal to square of the third side.

The given sides satisfies Pythagorean Theorem. So the given triangle is a right triangle.

Problem 12 :

14. The sides of a triangle are 5in, 5in and 5√2in. Check whether it is a right triangle.

Solution :

5² = 25, 5² = 25, (5√2)² = 50

25 + 25 = 50

5² + 5² = (5√2)²

Sum of squares of two sides is equal to square of the third side.

The given sides satisfies Pythagorean Theorem and also two of its sides are equal. So the given triangle is an isosceles right triangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6