AREA BOUNDED BY A CURVE AND THE Y AXIS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Let x = f(y) be a continuous function of y on [c, d] to the right of y-axis as shown below.
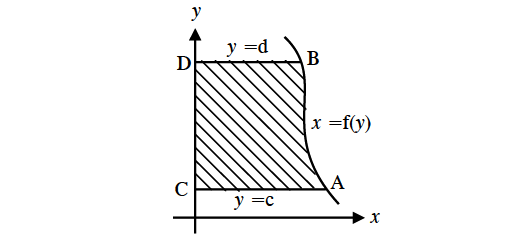
Then, the area bounded by the curve x = f(y) and the y-values y = c and y = d to the right of y-axis is given by
What if the curve lies to the left of y-axis between the lines y = c and y = d?
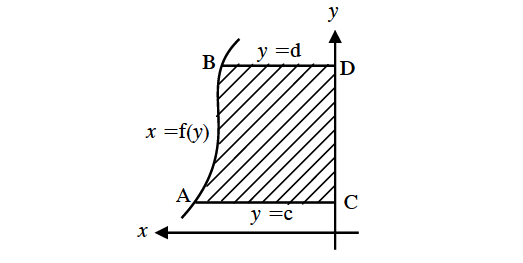
Then, the area bounded by the curve x = f(y) and the y-values y = c and y = d to the left of y-axis is given by
Example 1 :
Find the area of the region bounded by y = 2x + 1, y = 3, y = 5 and y–axis.
Solution :
The line y = 2x + 1 lies to the right of y-axis between the lines y = 3 and y = 5 as shown below.
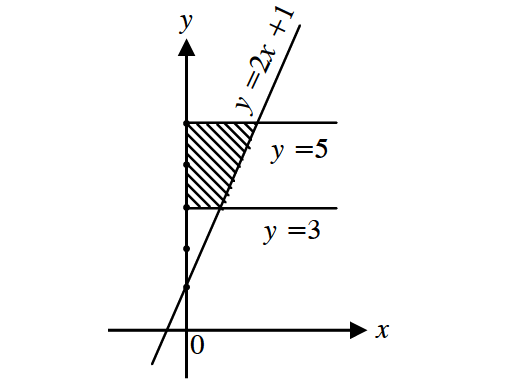
Solve the equation y = 2x + 1 for x in terms of y.
y = 2x + 1
y - 1 = 2x
⁽ʸ ⁻ ¹⁾⁄₂ = x
The required area :
Example 2 :
Find the area of the region bounded by y = 2x + 4, y = 1, y = 3 and y–axis.
Solution :
The line y = 2x + 4 lies to the left of y-axis between the lines y = 1 and y = 3 as shown below.
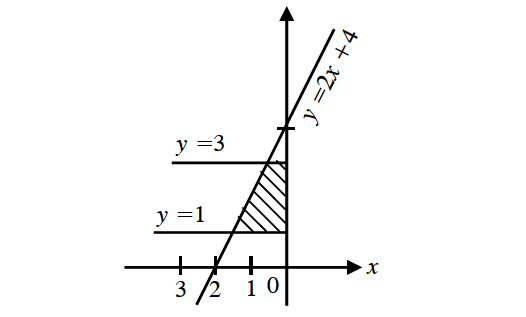
Solve the equation y = 2x + 4 for x in terms of y.
y = 2x + 4
y - 4 = 2x
⁽ʸ ⁻ ⁴⁾⁄₂ = x
The required area :
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus BC Problems with Solutions
Dec 20, 25 10:51 AM
AP Calculus BC Problems with Solutions -
AP Precalculus Problems and Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Precalculus Problems and Solutions (Part - 1) -
AP Calculus AB Problems with Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Calculus AB Problems with Solutions (Part - 1)
