AREA AND PERIMETER IN THE COORDINATE PLANE WORKSHEET

1. A gardener uses a coordinate grid to design a new garden. The gardener uses polygon WXYZ on the grid to represent the garden. The vertices of this polygon are W(3, 3), X(-3, 3), Y(-3, -3), and Z(3, -3). Each grid unit represents one yard. Find the area of the garden.

2. Caleb is planning a new deck for his house. He graphs the deck as polygon ABCDEF on a coordinate plane in which each grid unit represents one foot. The vertices of the polygon are A(1, 0), B(3, 2), C(3, 5), D(8, 5), E(8, 2), and F(6, 0). What is the area of Caleb’s deck ?

3. The grid shows the path Tommy followed when he walked from his home at (0, 0) to various locations and back home again. If each grid square represents one block, how many blocks did he walk ?

4. Suppose the next day Tommy walks from his home to the mall at (0, 8), and then walks to a movie theater at (7, 8). After leaving the theater Tommy walks to the store at (7, 0) before returning home. How far does he walk ?

1. Answer :

Step 1 :

Graph the vertices, and connect them in order.

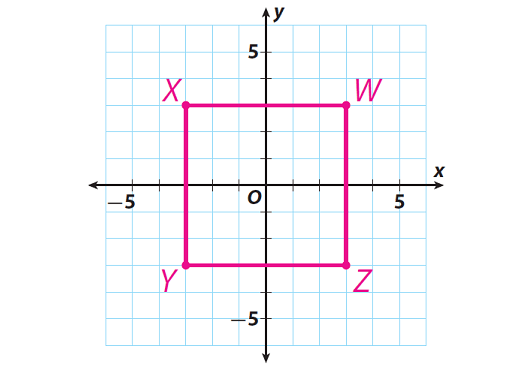
From the graph, it clear that the shape of the garden is a square. 

Let us find lengths of the sides YZ and WZ. 

Step 2 :

Find the length of the side YZ.

The ordered pair of Y is (-3, -3).

The x-coordinate of Y is -3, so point Y is |-3| = 3 yards from the y-axis.

The ordered pair of Z is (3, -3).

The x-coordinate of Z is 3, so point Z is |3| = 3 yards from the y-axis.

Find the sum of the distances :

The length of side YZ  =  3 + 3  =  6 yards

Step 3 :

Find the length of the side WZ.

The ordered pair of W is (3, 3).

The y-coordinate of W is 3, so point W is |3| = 3 yards from the x-axis.

The ordered pair of Z is (3, -3).

The y-coordinate of Z is -3, so point Z is |3| = 3 yards from the x-axis.

Find the sum of the distances :

The length of side WZ  =  3 + 3  =  6 yards.

Step 4 :

Find the area of the square WXYZ using the lengths of the sides YZ and WZ.

Area of the square WXYZ  =  side x side

Area of the square WXYZ  =  YZ x WZ

Area of the square WXYZ  =  6 x 6

Area of the square WXYZ  =  36 square yards.

2. Answer :

Step 1 :

Graph the vertices, and connect them in order.

Draw a horizontal dashed line segment to divide the polygon into two quadrilaterals — a rectangle and a parallelogram.

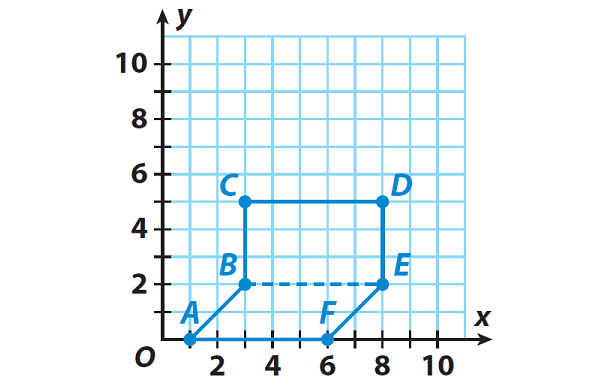
Step 2 :

Find the area of the rectangle using the length of segment BE as the base b and the length of segment BC as the height h.

b  =  |8| - |3|  =  5 feet

h  =  |5| - |2|  =  3 feet

A  =  bh  =  5 x 3  =  15 square feet

Step 3 :

Find the area of the parallelogram using the length of segment AF as the base. Use the length of a segment from F(6, 0) to the point (6, 2) as the height h.

b  =  |6| - |1|  =  5 feet

h  =  |2| - 0  =  2 feet

A  =  bh  =  5 x 2  =  10 square feet

Step 4 :

Add the areas to find the total area of the deck.

hence, the required area is

=  15 + 10

=  25 square feet

3. Answer :

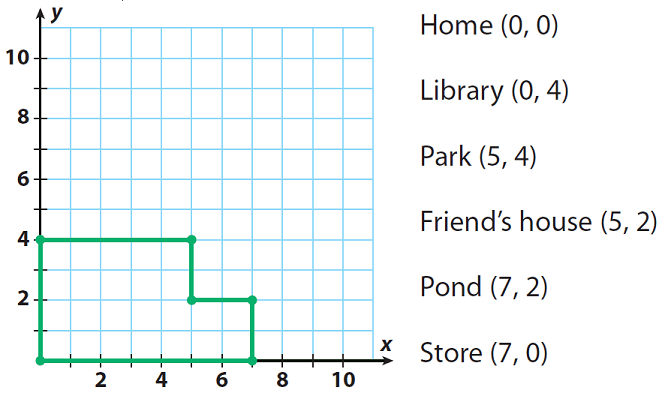
Step 1 :

Find each distance. Each grid unit represents one block.

Tommy’s home (0, 0) to the library (0, 4) is 

|4| - 0  =  4 - 0  =  4 blocks.

The library (0, 4) to the park (5, 4) is

|5| - 0  =  5 - 0  =  5 blocks.

The park (5, 4) to Tommy’s friend’s house (5, 2) is

|4| - |2|  =  4 - 2  =  2 blocks.

Tommy’s friend’s house (5, 2) to the pond (7, 2) is

|7| - |5|  =  7 – 5  =  2 blocks.

The pond (7, 2) to the store (7, 0) is

|2| - 0  =  2 - 0  =  2 blocks.

The store (7, 0) to Tommy’s home (0, 0) is

|7| - 0  =  7 - 0  =  7 blocks

Step 2 :

Find the sum of the distances.

Tommy walked 4 + 5 + 2 + 2 + 2 + 7  =  22 blocks.

4. Answer :

The given situation has been illustrated in the graph given below.

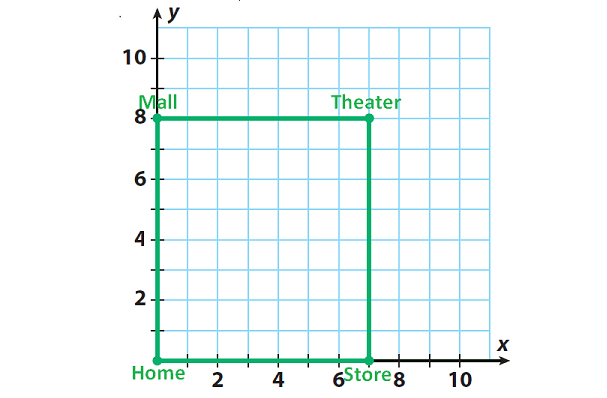
Step 1 :

Find each distance. Each grid unit represents one block.

Tommy’s home (0, 0) to the mall (0, 8) is 

|8| - 0  =  8 - 0  =  8 blocks.

The mall (0, 8) to the theater (7, 8) is

|7| - 0  =  7 - 0  =  7 blocks.

The theater (7, 8) to the store (7, 0) is

|8| - 0  =  8 - 0  =  8 blocks.

The store (7, 0) to Tommy’s home (0, 0) is

|7| - 0  =  7 - 0  =  7 blocks

Step 2 :

Find the sum of the distances.

Tommy walked 8 + 7 + 8 + 7  =  30 blocks.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.