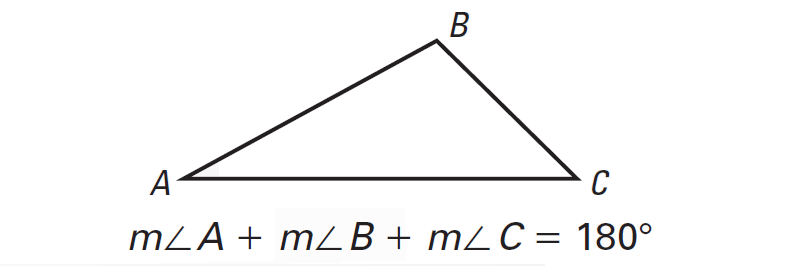AREA AND PERIMETER
Area :
The amount of space inside the boundary of a two- dimensional shape such as a triangle or circle.
Perimeter :
Perimeter is the distance around a two-dimensional shape such as square or rectangle or triangle.
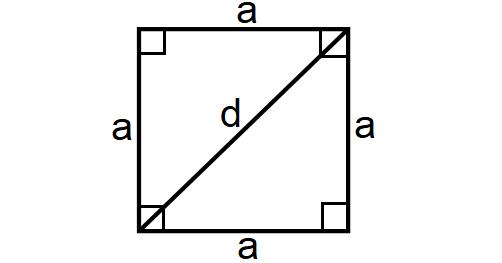
Square
A square is a four-sided polygon where the lengths of all the four sides will be equal and each vertex angle will be right angle or 90° as shown below.
When the side length is given :
Area of a Square = a2
When the length of the diagonal is given :
Area of a Square = 1/2 ⋅ d2
Perimeter of a Square = 4a
Rectangle
A rectangle is a four-sided polygon where the lengths of opposite sides will be equal and each vertex angle will be 90° or right angle as shown below.
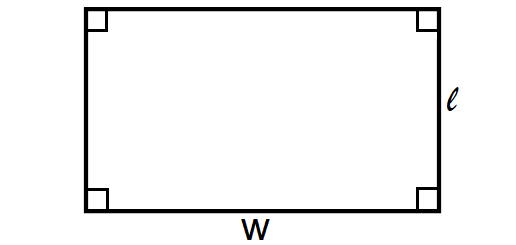
Area of a Rectangle = l ⋅ w
Perimeter of a Rectangle = 2(l + w)
Equilateral Triangle
An equilateral triangle is a three-sided polygon where the lengths of all the three sides will be equal and each vertex angle will be 60° as shown below.
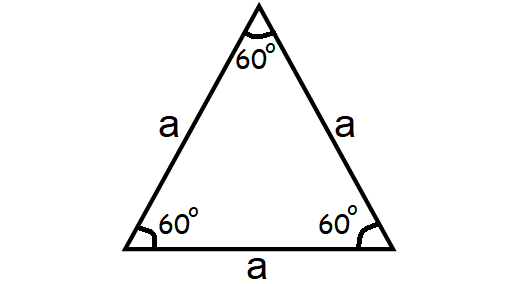
Area of an Equilateral Triangle = √3/4 ⋅ a2
Perimeter of an Equilateral Triangle = 3a
Scalene Triangle
An scalene triangle is a three-sided polygon where the all the three sides will have unequal lengths and the measures of all the three angles will be different as shown below.
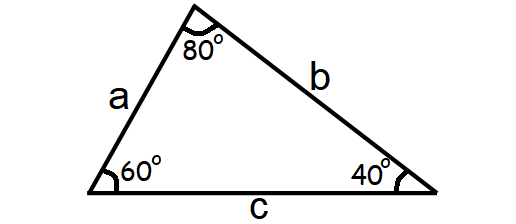
Area of a Scalene Triangle = √[s(s - a)(s - b)(s - c)]
where s = (a + b + c)/2
Perimeter of a Scalene Triangle = a + b + c
Quadrilateral
A quadrilateral is a four-sided polygon as shown below.
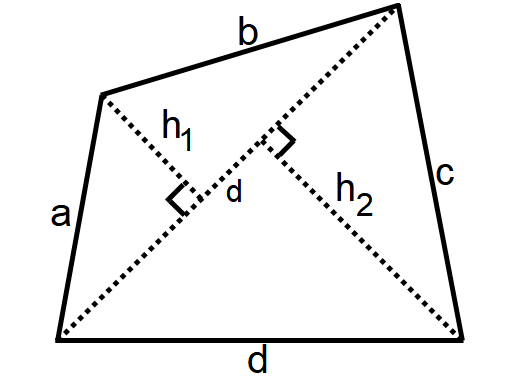
Area of a Quadrilateral = 1/2 ⋅ d ⋅ (h1 + h2)
Perimeter of a Quadrilateral = a + b + c + d
Parallelogram
A parallelogram is a four-sided polygon where the opposite sides will be equal and parallel as shown below.
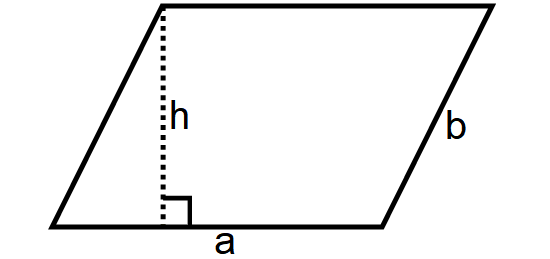
Area of a Parallelogram = b ⋅ h
Perimeter of a Parallelogram = 2(a + b)
Rhombus
A rhombus is a four-sided polygon where the lengths of all the four sides will be equal and opposite sides will be parallel as shown below.
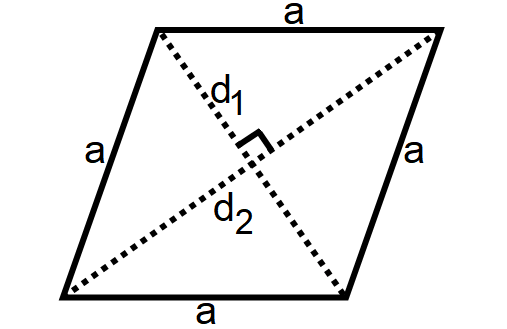
Area of a Rhombus = 1/2 ⋅ d1 ⋅ d2
Perimeter of a Rhombus = 4a
Trapezoid
A trapezoid is a four-sided polygon which has a pair of opposite sides parallel as shown below.
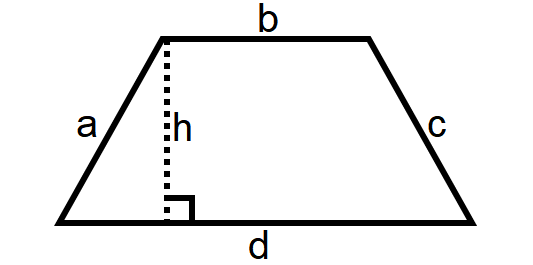
Area of a Trapezoid = 1/2 ⋅ h ⋅ (a + b)
Perimeter of a Trapezoid = a + b + c + d
Circle
A circle is a round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center). The distance between the center and any point on the circumference is called radius (r).
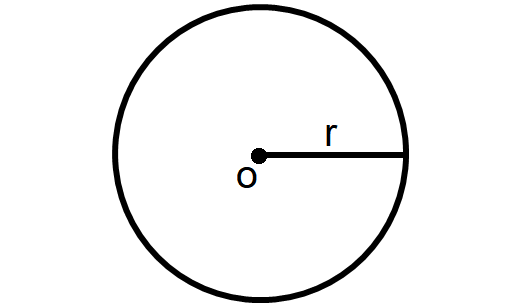
Area of a Circle = πr2
Perimeter of a Circle = 2πr
Semicircle
A semicircle is a half of a circle or of its circumference as shown below.
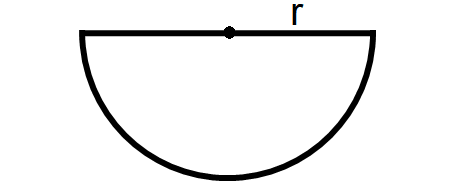
Area of a Semicircle = πr2/2
Perimeter of a Semicircle = πr + 2r
Quadrant
A quadrant is a one-fourth of a circle.
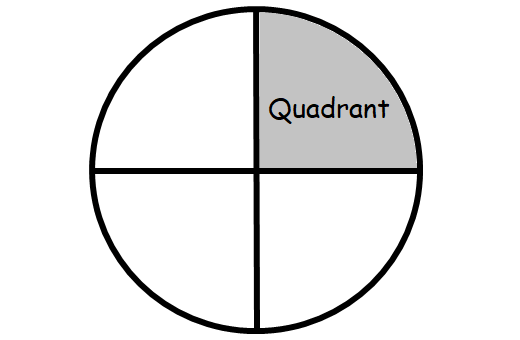
Area of a Quadrant = πr2/4
Perimeter of a Quadrant = πr/2 + 2r
Sector of a Circle
A sector of a circle is a part of the interior of the circle enclosed by an arc and two radii.
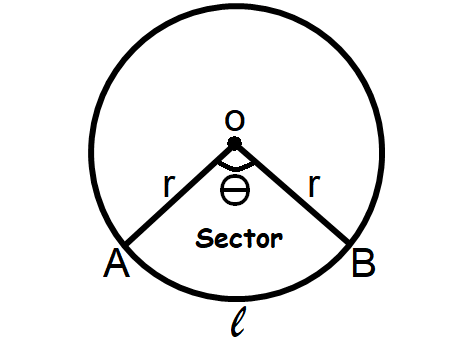
Area of a Sector = θ/360° ⋅ πr2
Length of the Arc AB = θ/360° ⋅ 2πr
Perimeter a Sector = (θ/360° ⋅ 2πr) + 2r
Regular Polygon
A regular polygon is a polygon that is equiangular (all interior angles are equal in measure) and equilateral (all sides have the same length).
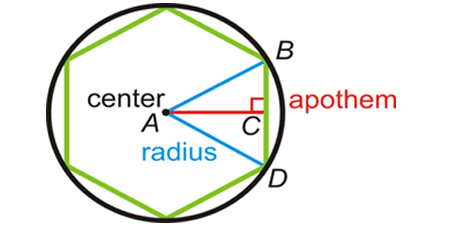
Area = 1/2 ⋅ (Apothem x Perimeter)
Perimeter = No. of sides ⋅ Length of each side
Solved Problems
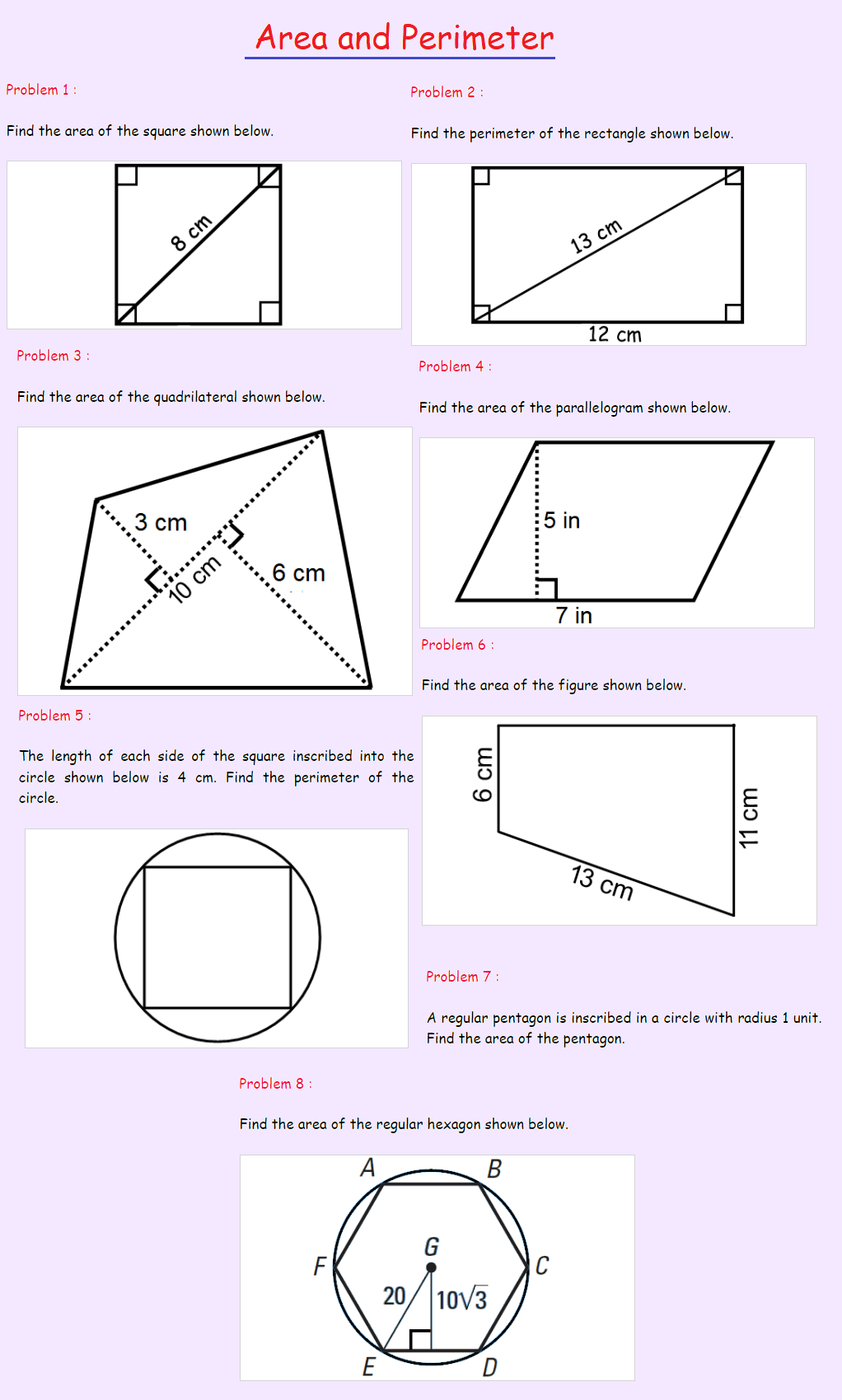
Problem 1 :
If the length of each side of a square is 5 cm, find its perimeter.
Solution :
Perimeter of the square = 4 x length of each side
= 4 x 5
= 20 cm
Problem 2 :
If the length and width of a rectangle are 4.2 in. and 7 in. respectively. Find its area.
Solution :
Area of the rectangle = length x width
= 4.2 x 7
= 29.4 in.2
Problem 3 :
The length of a rectangle is 3 more than twice the width. If the perimeter of the rectangle is 36 cm, find the length and width of the rectangle.
Solution :
Let x be the width of the rectangle.
Then, length of the rectangle :
= 2x + 3
Perimeter of the rectangle = 36 cm
2(length + width) = 36
2(2x + 3 + x) = 36
2(3x + 3) = 36
Divide both sides by 2.
3x + 3 = 18
Subtract 3 from both sides.
3x = 15
Divide both sides by 3.
x = 5
2x + 3 = 2(5) + 3
2x + 3 = 10 + 3
2x + 3 = 13
Length and width of the rectangle are 13 cm and 5 cm respectively.
Problem 4 :
Find the area of a circle whose radius is 7 cm. Use π = 3.14 and round your answer to the nearest tenth.
Solution :
Area of the circle = πr2
= 3.14 x 72
= 3.14 x 49
= 153.9 cm2
Problem 5 :
If the radius of a circle is 6.5 in., find its circumference. Use π = 3.14 and round your answer to the nearest tenth.
Solution :
Circumference of the circle = 2πr
= 2 x 3.14 x 6.5
= 40.82 in.
Click here to get detailed answers for the above questions.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Sum of the Three Angles of a Triangle
Apr 26, 24 09:20 PM
Sum of the Three Angles of a Triangle - Concept - Solved Examples -
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems