APPLYING SCALE FACTORS TO FIND AREA PERIMETER AND VOLUME

A scale factor is a factor by which all the components of an object multiplied in order to create proportional enlargement or reduction.

Example 1 :

Two similar solids have side lengths in the ratio 2 : 5.

(a)  What is the ratio of their volumes ?

(b)  If the smaller shape has a volume of 100 mm³, what is the shape of the larger shape ?

Solution :

(a)  If two shapes are in the ratio a : b, then ratio of their volumes is a³ : b³.

Ratio of its volume  =  2³ : 5³

=  8 : 125

(b)  Volume of the smaller shape  =  100 mm³

Ratio of their volume  =  (Ratio of the sides)³

Volume of smaller shape/Volume of larger shape  =  (2/5)³

100/Volume of larger shape  =  8/125

Volume of larger shape  =  100(125)/8

=  1562.5 cm³

Example 2 :

Two similar solids have volumes of 20 m³ and 1280 m³. James says that the sides of the larger solids are 4 times as long as the sides of the smaller shape. Claire says that the sides are  8 times longer. Who is correct ?

Solution :

Ratio of volume of solids  =  20/1280

=  1/64

(a/b)³  =  (1/64)

(a/b)³  =  (1/4)³

Volume of smaller shape / Volume of larger shape  =  1/64

 Volume of Larger shape  =  4 x Volume of smaller shape

So, James is correct.

Example 3 :

Find the values of x and y and the measure the angle P.

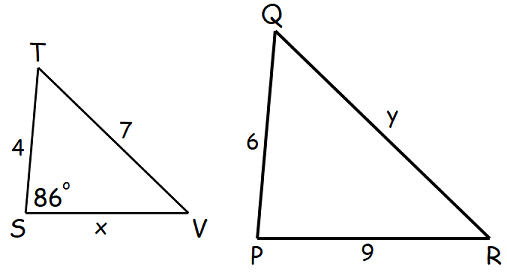
Solution :

TS/QP  = TV/QR  =  SV/PR

4/6  =  7/y  =  x/9

2/3  =  7/y  =  x/9

In the similar figures, the side length may change the angle measure does not.

So angle P is also 86 degree.

Example 4 :

Two polygons are similar. If the ratio of their perimeters is 3 : 4, find the ratio of the corresponding sides.

Solution :

Ratio of the corresponding sides  =  Ratio of their perimeter

Ratio of the corresponding sides  =  3 : 4

Example 5 :

Two polygons are similar. If the ratio of the area is 100 : 49, find the ratio of their corresponding sides.

Solution :

Ratio of areas of similar figures 

=  (Ratio of the corresponding sides)² 

Let a and b be the corresponding sides.

100 : 49  =  (a : b)²

10 : 7  =  a : b

Ratio of corresponding sides is 10 : 7.

Example 6 :

Two triangles are similar and the perimeter of the smaller one is 50. The ratio of the corresponding sides is 3 : 4, find the perimeter of the larger triangle.

Solution :

Ratio of corresponding sides  =  Ratio of their perimeter

3 : 4  =  Perimeter of smaller triangle : perimeter of larger triangle

3/4  =  Perimeter of smaller triangle/Perimeter of the larger

3/4  =  50/Perimeter of larger triangle

Perimeter of larger triangle  =  50(4)/3

=  66.67

Example 7 :

2 triangles are similar and a side of the smaller one is 8. The ratio of the corresponding areas is 25:36, find the length of the corresponding side of the larger triangle.

Solution :

(Ratio of corresponding side)²  =  Ratio of their areas 

Let a and b be the corresponding sides.

(a:b)²  =  25 : 36

a:b  =  √(25:36)

Ratio of the corresponding sides is 5 : 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.