ANGLES IN A CYCLIC QUADRILATERAL WORKSHEET

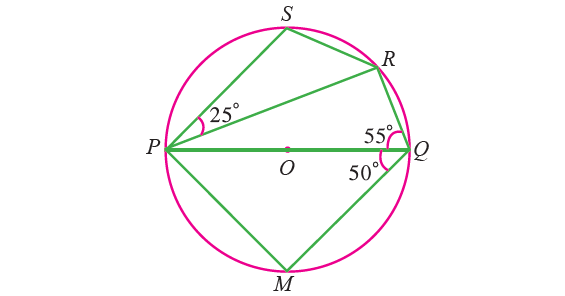
1. In the figure given below, PQ is a diameter of a circle with center O. If ∠PQR = 55°, ∠SPR = 25° and ∠PQM = 50°. Find :

(i) ∠QPR

(ii) ∠QPM

(iii) ∠PRS. 

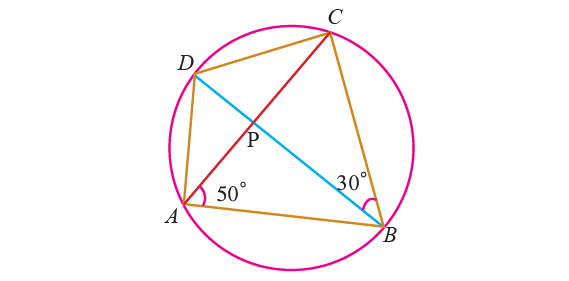
2. In the figure shown below, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that ∠DBC = 30° and ∠BAC = 50°. Find :

(i) ∠BCD 

(ii) ∠CAD

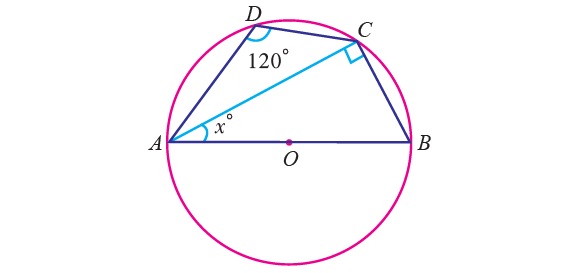
3. In the figure given below, O is the center of a circle and ∠ADC = 120°. Find the value of x.

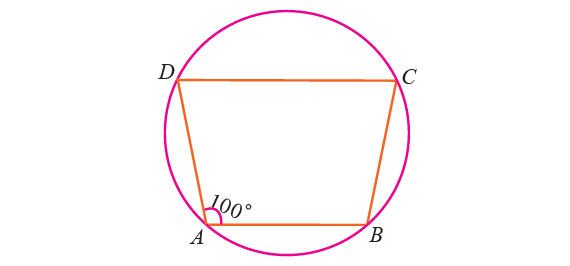
4. In the figure given below, ABCD is a cyclic quadrilateral in which AB || DC. If ∠BAD = 100° find

(i) ∠BCD

(ii) ∠ADC

(iii) ∠ABC

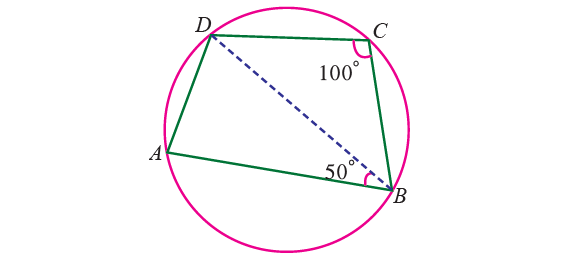
5. In the figure given below, ABCD is a cyclic quadrilateral in which ∠BCD = 100° and ∠ABD = 50° find ∠ADB. 

6)  Find the value of ∠PQR if PS || RQ and PQRS is cyclic quadrilateral.

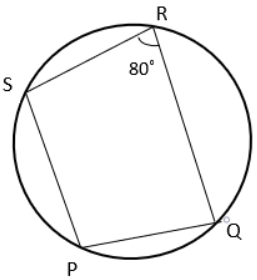
a) 45°     b) 50°    c) 80°    d) 90°

7)   What is the value of x if ∠AOC if ABCD is cyclic quadrilateral?

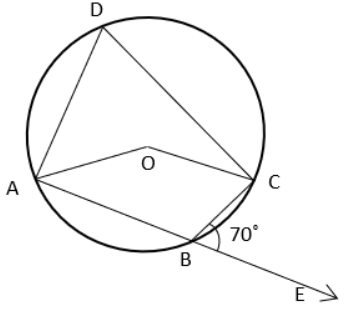
a) 140°       b) 110°     c) 70°     d) 45°

8)  From the figure given below, ∠PAB = __________

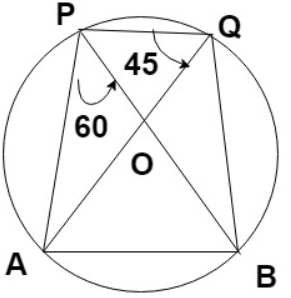
a) 90°     b) 110°    c) 95°     d) 75°

9)  Find x and y giving reasons for your answers :

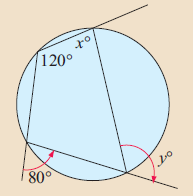
10) Find x and y.

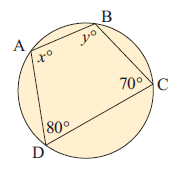
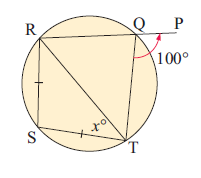
11)  Find x.

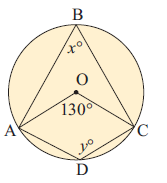
12) Find the values of x and y.

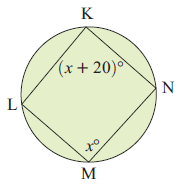
13)  Find x.

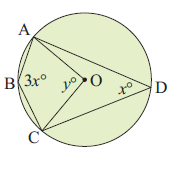
14) Find the values of x and y.

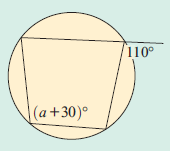
15) Find the value of a.

1. Answer :

(i) ∠PRQ = 90° (angles in a semi circle is a right angle)

In triangle PRQ,

∠PRQ + ∠QPR + ∠PQR = 180°

90° + ∠QPR + 55° = 180°

145° + ∠QPR  = 180°

∠QPR  =  35°

(ii)  In triangle QPM,

∠QPM + ∠MQP + ∠QMP = 180°

∠QPM + 50° + 90° = 180°

∠QPM + 140° = 180°

∠QPM = 40°

(iii) ∠PQR + ∠PSR = 180

55 + ∠PSR = 180°

∠PSR =  125°

In triangle PSR,

∠PSR + ∠SPR + ∠PRS  =  180°

125° + 25° + ∠PRS  =  180°

150° + ∠PRS  =  180°

∠PRS  =  30°

2. Answer :

Angles in the same segment must be equal

So, ∠CBD and ∠CAD are equal.

∠CAD = ∠CBD = 30°

∠DAB + ∠DCB = 180

∠DAC + ∠CAB + ∠BCD = 180°

30° + 50° + ∠BCD = 180°

80° + ∠BCD = 180°

∠BCD = 100°

3. Answer :

In the figure given below, O is the center of a circle and ∠ADC = 120°. Find the value of x.

ABCD is a cyclic quadrilateral. we have

∠ABC + ∠ADC = 180°

∠ABC + 120° = 180°

∠ABC = 60°

Also ∠ACB = 90° (angle on a semi circle)

In triangle ABC we have,

∠BAC + ∠ACB + ∠ABC = 180°

∠BAC + 90° + 60° = 180°

∠BAC + 150° = 180°

∠BAC = 30°

Hence the value of x is 30.

4. Answer :

∠BAD + ∠BCD = 180°

100° + ∠BCD = 180°

∠BCD = 80°

∠ADC = 80°

∠ADC + ∠ABC = 180°

80° + ∠ABC = 180°

∠ABC = 100°

5. Answer :

∠DAB + ∠DCB = 180°

∠DAB + 100° = 180°

∠DAB = 80°

In triangle ADB,

∠DAB + ∠ABD + ∠BDA = 180°

80° + 50° + ∠ADB = 180°

130° + ∠ADB = 180°

∠ADB = 50°

6. Answer :

∠P + ∠R = 180

∠P + 80 = 180

∠P = 180 - 80

∠P = 100

7. Answer :

∠ABC + ∠CBE = 180

∠ABC + 70 = 180

∠ABC  = 180 - 70

∠ABC  = 110

∠ADC + ∠ABC = 180

∠ADC + 110 = 180

∠ADC = 180 - 110

∠ADC = 70

8. Answer :

∠APB = ∠AQB

Angle lies in the same segment will be equal.

∠APB = ∠AQB = 60

∠PQB = ∠PQA + ∠AQB

∠PQB = 45 + 60

∠PQB = 105

∠PAB + ∠PQB = 180

∠PAB + 105 = 180

∠PAB = 180 - 105

∠PAB = 75

9. Answer :

Exterior angles of cyclic quadrilateral are equal.

x = 80 and y = 120

10. Answer :

So, the values of x and y are 110 and 100 degree.

11. Answer :

∠SRT = x = ∠STR

∠RST = ∠RQT

∠RST = 180 - 100

∠RST = 80

In a triangle RST,

∠RST + ∠STR + ∠TRS = 180

80 + x + x = 180

2x = 180 - 80

2x = 100

x = 100/2

x = 50

So, the value of x is 50 degree.

12. Answer :

∠AOC = 2∠ABC

∠AOC = 2x

130 = 2x 

x = 130/2

x = 65

In a cyclic quadrilateral, the sum of opposite angles is equal to 180 degree.

x + y = 180

65 + y = 180

y = 180 - 65

y = 115

13. Answer :

∠M + ∠K = 180

x + x + 20 = 180

2x + 20 = 180

2x = 180 - 20

2x = 160

x = 160/2

x = 80

So, the value of x is 80.

14. Answer :

y = 2x

x + 3x = 180

4x = 180

x = 180/4

x = 45

Applying the value of x, we get

y = 2(45)

y = 90

15. Answer :

a + 30 = 110

a = 110 - 30

a = 80

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.