ANGLE OF ELEVATION WORD PROBLEMS WORKSHEET

(1)  Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height 10√3 m.      Solution

(2)  A road is flanked on either side by continuous rows of houses of height 4 √3 m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30° . Find the width of the road.                     Solution

(3)  To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? (√3 = 1.732)            Solution

(4)  A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 40° . Find the height of the pedestal. (tan 40° = 0.8391, √3 = 1.732)

Solution

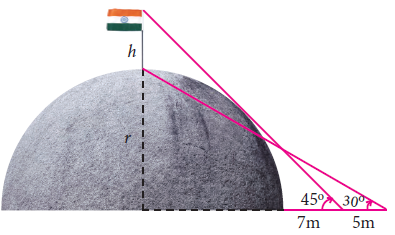
(5)  A flag pole ‘h’ meters is on the top of the hemispherical dome of radius ‘r’ meters. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30° . Find (i) the height of the pole (ii) radius of the dome. (√3 = 1.732)   

Solution 

(6)  A vertical pole fixed to the ground is divided in the ratio 1:9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 25 m away from the base of the pole, what is the height of the pole?          Solution 

(7)  The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?         Solution 

(8)  A traveler approaches a mountain on highway. He measures the angle of elevation to the peak at each milestone. At two consecutive milestones the angles measured are 4° and 8° . What is the height of the peak if the distance between consecutive milestones is 1 mile. (tan 4° = 0.0699, tan 8° = 0.1405)         Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.