QUESTIONS BASED ON ANGLE OF ELEVATION

Question 1 :

To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? (√3 = 1.732)

Solution :

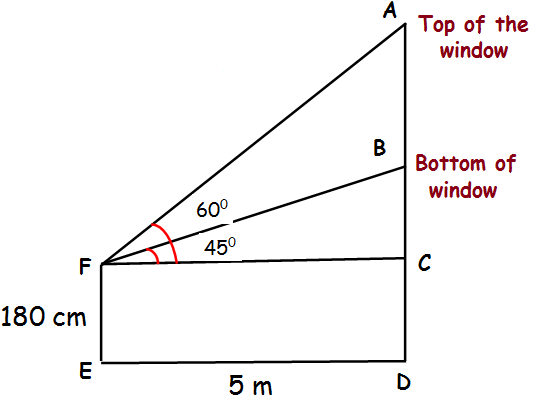
Height of window  =  AB

180 cm  =  1.8 m

In triangle FBC,

tan θ  =  Opposite side / Adjacent side 

tan 45  =  BC/FC

1  =  BC/5

BC  =  5 m

In triangle FBC,

tan 60  =  AC/FC

√3  =  AC/5

AC  =  5√3

AB  =  AC - BC

  =  5√3 - 5

  =  5(√3 - 1)

  =  5(1.732 - 1)

  =  5(0.732)

  =  3.66 m 

Hence height of window is 3.66 m.

Question 2 :

A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 40° . Find the height of the pedestal. (tan 40° = 0.8391, √3 = 1.732)

Solution :

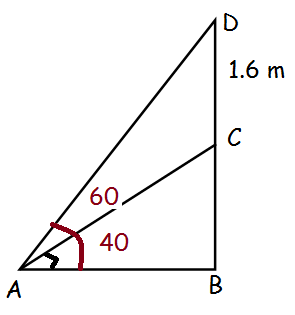
In triangle ABC, 

tan θ  =  Opposite side / Adjacent side 

tan 40  =  BC/AB

0.8391  =  BC/AB

Let BC = x

0.8391  =  x/AB

AB  =  x/0.8391  -----(1)

In triangle ABD,

tan 60  =  BD/AB

√3  =  (1.6 + x)/AB

AB  =  (1.6 + x)/√3 -----(2)

(1)  =  (2)

x/0.8391  =  (1.6 + x)/√3

√3x  =  (1.6 + x) 0.8391

1.732x - 0.8391x  =  1.6(0.8391)

 0.8929x  =  1.34256

x  =  1.34256/0.8929

x  =  134256/89290

Hence the height of the pedestal is 1.5 m.

Question 3 :

A flag pole ‘h’ meters is on the top of the hemispherical dome of radius ‘r’ meters. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30° . Find (i) the height of the pole (ii) radius of the dome. (√3 = 1.732)

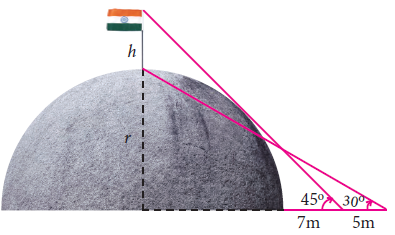
Solution :

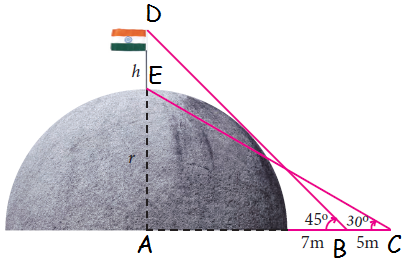
In triangle ADB, 

tan θ  =  Opposite side / Adjacent side 

tan 45  =  (r + h)/AB

1  =  (r + h)/(r + 7)

r + h = r + 7

r - r + h =  7

h = 7 m

In triangle ADC,

tan 30  =  AE/AC

1/√3  =  r / (r + 12)

r + 12  =  √3r

r(1 - √3)  =  -12

r = [12/(√3 - 1)]  [(√3 + 1)/(√3 + 1)]

  =  12(√3 + 1)/2

  =  6(1.732 + 1)

  =  6(2.732)

r  =  16.39 m

(i) the height of the pole = 7m

(ii) radius of the dome  =  16.39 m

Question 4 :

A tree is struck by lightning and snaps off 34 feet above the ground. The top part of the tree, 117 feet long, rests with the tip on the ground whole the broken end rests on the top of the stump. What angle does the top part of the tree make with the ground?

Solution :

Opposite side = 34 ft

Length of tree from broken part to the top of the tree

= 117 ft

sin x = Opposite side / Hypotenuse

sin x = 34/117

sin x = 0.29

x = sin ^-1(0.29)

x = 16.85

So, the required angle measure is approximately 16.9 

Question 5 :

The angle of elevation from D to B is 30°. The angle of elevation from D to C is 45°. AD is 20m . Find the distance from B to C.

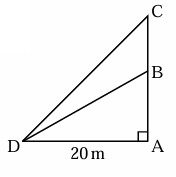
Solution :

<BDA = 30

<CDA = 45

AD = 20 m

In triangle DBA,

tan 30 = BA/DA

1/√3 = BA/20

BA = 20/√3

BA = 11.54

In triangle CDA

tan 45 = CA/DA

Let CB = x

1 = (CB + BA)/20

1 = (x + 11.54)/20

x + 11.54 = 20

x = 20 - 11.54

x = 8.46 m

So, the measure of BC is 8.46 m.

Question 6 :

A 200 ft high television transmitting tower is to be supported by guy wires running from the ground to the top of the tower. The wires make an angle of 63 with the ground.

a) How long is each wire?

b) How far from the base of the tower must they meet the ground?

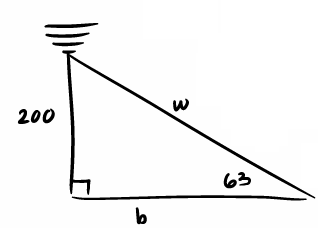
Solution :

Question 7 :

A woman is standing on the ground at a point 78ft from the base of a building. The angle of elevation to the top of the building is 57. To the nearest foot, how high is the building?

Solution :

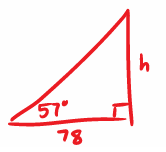
tan 57 = h/78

1.53 = h/78

h = 1.53(78)

= 119.34 ft

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.