ANGLE BISECTORS OF A TRIANGLE WORKSHEET

Problems 1-6 : Each figure shows a triangle with one of its angle bisectors (in blue color).

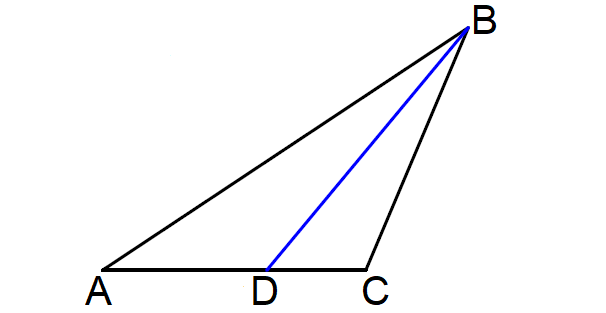
Problem 1 :

In ΔABC below, if m∠ABC = 34°, find m∠ABD.

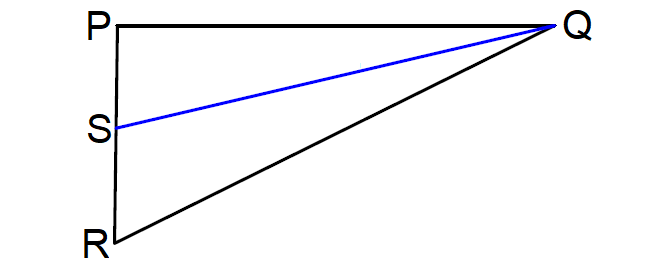
Problem 2 :

In ΔPQR below, if m∠SQR = 13°, find m∠PQR.

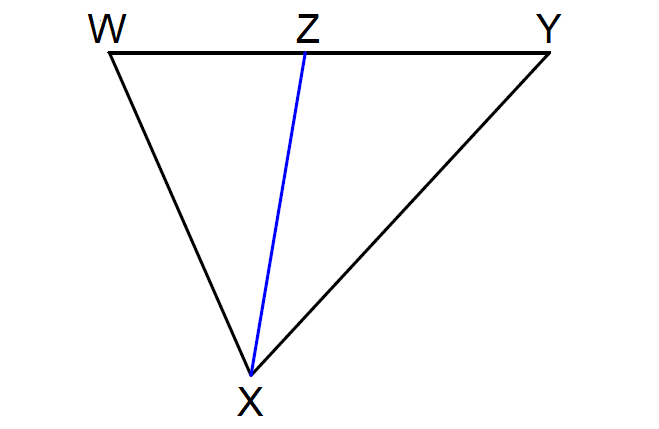
Problem 3 :

In ΔWXY below, solve for x, if

m∠WXZ = (4x + 5)°

m∠ZXY = (5x - 2)°

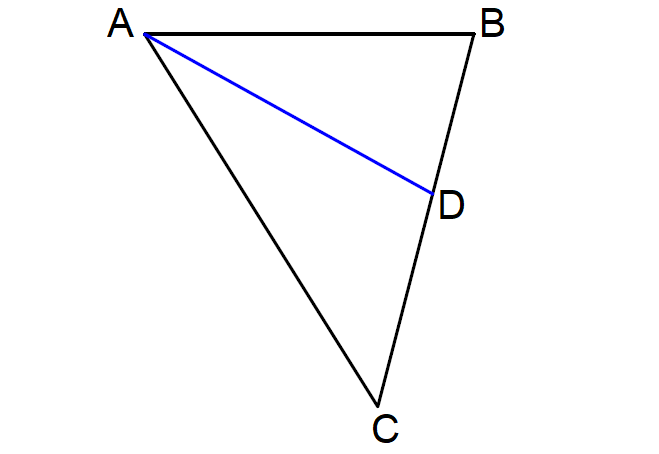
Problem 4 :

In ΔABC below, solve for x, if

m∠BAD = (1 + 28x)°

m∠BAC = (59x - 1)°

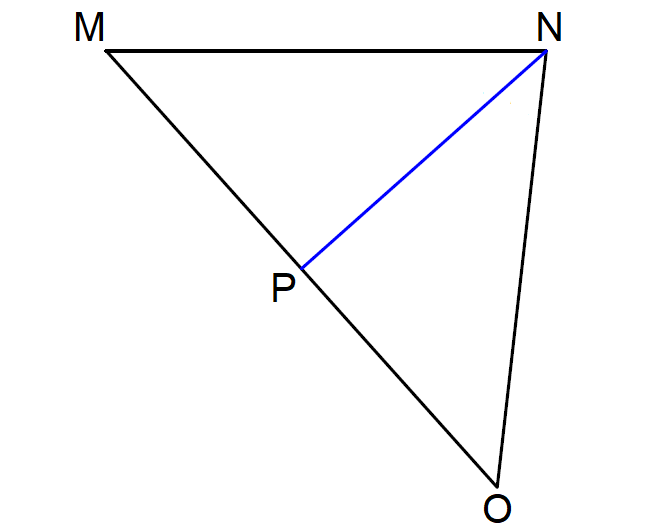
Problem 5 :

In ΔMNO below, solve for x, if

m∠MNP = (7x + 7)°

m∠MNO = (16x + 4)°

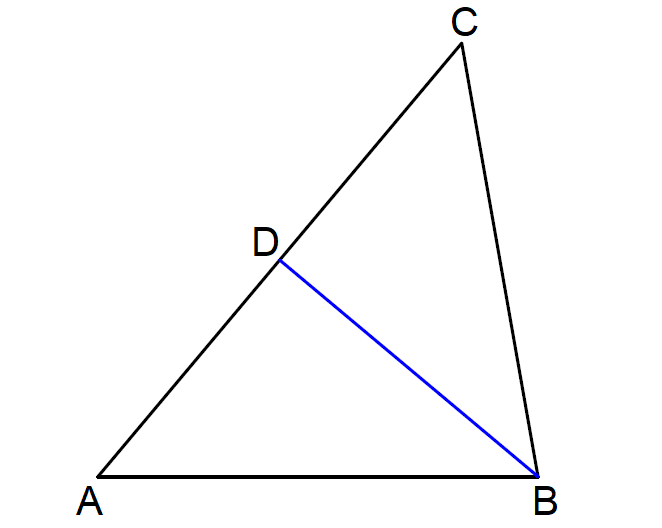
Problem 6 :

In ΔABC below, find m∠ABC, if

m∠ABD = (7x + 5)°

m∠DBC = (9x - 5)°

Problems 7-12 : Each figure shows a triangle with one of its angle bisectors (in blue color).

Problem 7 :

In ΔABC below, if MD = 3, find ME.

Problem 8 :

In ΔJKL below, if MQ = 7, find RM.

Problem 9 :

In ΔABC below, if RM = 5, find QM.

Problem 10 :

In ΔDEF below, if CD = 2 and DM = 3, find MB.

Problem 11 :

In ΔWXY below, if MQ = 3 and XQ = 4, find XM.

Problem 12 :

In ΔSTU below, if MK = 1 and SL = 2, find SM.

Answers

1. Answer :

In ΔABC above, since BD is the angle bisector of ∠ABC,

m∠ABD = 17°

2. Answer :

In ΔPQR above, since QS is the angle bisector of ∠PQR,

m∠PQS = m∠SQR

m∠PQS = 13°

m∠PQR = m∠PQS + m∠SQR

m∠PQR = 13° + 13°

m∠PQR = 26°

3. Answer :

In ΔWXY above, since XZ is the angle bisector of ∠WXY,

m∠WXZ = m∠ZXY

(4x + 5)° = (5x - 2)°

4x + 5 = 5x - 2

-x = -7

x = 7

4. Answer :

In ΔABC above, since AD is the angle bisector of ∠BAC,

m∠BAD = m∠DAC

m∠BAD = (1 + 28x)°

m∠BAC = m∠BAD + m∠DAC

(59x - 1)° = (1 + 28x)° + (1 + 28x)°

59x - 1 = 1 + 28x + 1 + 28x

59x - 1 = 56x + 2

3x = 3

x = 1

5. Answer :

In ΔMNO above, since NP is the angle bisector of ∠MNO,

m∠PNO = m∠MNP

m∠PNO = (7x + 7)°

m∠MNO = m∠MNP + m∠PNO

(16x + 4)° = (7x + 7)° + (7x + 7)°

16x + 4 = 7x + 7 + 7x + 7

16x + 4 = 14x + 14

2x = 10

x = 5

6. Answer :

In ΔABC above, since BD is the angle bisector of ∠ABC,

m∠ABD = m∠DBC

(7x + 5)° = (9x - 5)°

7x + 5 = 9x - 5

-2x = -10

x = 5

x = 7

m∠ABC = m∠ABD + m∠DBC

m∠ABC = (7x + 5)° + (9x - 5)°

Substitute x = 5.

m∠ABC = (7 ⋅ 5 + 5)° + (9 ⋅ 5 - 5)°

m∠ABC = (35 + 5)° + (45 - 5)°

m∠ABC = 40° + 40°

m∠ABC = 80°

7. Answer :

In ΔABC above, since AM, BM and CM are angle bisectors,

MD = ME = MF

Since MD = 3,

ME = 3

8. Answer :

In ΔJKL above, since JM, KM and LM are angle bisectors,

MP = MQ = MR

Since MQ = 7,

MR = 7

or

RM = 7 

9. Answer :

In ΔABC above, since AM, BM and CM are angle bisectors,

PM = QM = RM

Since RM = 5,

QM = 5

10. Answer :

In ΔDEF above, since DM, EM and FM are angle bisectors,

MA = MC = MB

In right triangle DMC, using Pythagorean Theorem,

MC² + CD² = DM²

MC² + 2² = 3²

MC² + 4 = 9

MC² = 5

MC = √5

Since MA = MC = MB,

MB = √5

11. Answer :

In right triangle MQX, using Pythagorean Theorem,

XM² = XQ² + MQ²

XM² = 3² + 4²

XM² = 9 + 16

XM² = 25

XM² = 5²

XM = 5

12. Answer :

In ΔSTU above, since SM, TM and UM are angle bisectors,

MJ = MK = ML

Since MK = 1,

ML = 1

In right triangle SML, using Pythagorean Theorem,

SM² = SL² + ML²

SM² = 2² + 1²

SM² = 4 + 1

SM² = 5

SM = √5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.