ADDING AND SUBTRACTING FRACTIONS

Adding and Subtracting Like Fractions

Example 1 :

Add 1/7 and 3/7.

Solution :

= 1/7 + 3/7

The given fractions are like fractions (having same denominator). To add them, take the denominator once and combine the numerators.

= (1 + 3)/7

= 4/7

Example 2 :

Subtract 2/9 from 5/9.

Solution :

= 5/9 - 2/9

= (5 - 2)/9

= 3/9

= 1/3

Example 3 :

Simplify :

4/5 + 2/5 - 3/5

Solution :

= 4/5 + 2/5 - 3/5

= (4 + 2 - 3)/5

= 3/5

Adding and Subtracting Unlike Fractions

Example 4 :

Add 3/4 and 5/6.

Solution :

The given fractions are unlike fractions (having different denominators).

Least common multiple of (4, 6) = 12.

To make the denominator as 12, multiply both numerator and denominator of the first fraction by 3 and the second fraction by 2.

3/4 = (3 x 3)/(4 x 3) = 9/12

5/6 = (5 x 2)/(6 x 2) = 10/12

3/4 + 5/6 :

= 9/12 + 10/12

= (9 + 10)/12

= 19/12

Example 5 :

Subtract 1/9 from 5/6.

Solution :

Least common multiple of (9, 6) = 18.

To make the denominator as 18, multiply both numerator and denominator of the first fraction by 2 and the second fraction by 3.

1/9 = (1 x 2)/(9 x 2) = 2/18

5/6 = (5 x 3)/(6 x 3) = 15/18

5/6 - 1/9 :

= 15/18 - 2/18

= (15 - 2)/18

= 13/18

Example 6 :

Simplify :

3/4 + 1/6 - 5/8

Solution :

Least common multiple of (4, 6, 8) = 24.

To make the denominator as 24, multiply both numerator and denominator of the first fraction by 6, second fraction by 4 and the third fraction by 3.

3/4 = (3 x 6)/(4 x 6) = 18/24

1/6 = (1 x 4)/(6 x 4) = 4/24

5/8 = (5 x 3)/(8 x 3) = 15/24

3/4 + 1/6 - 5/8 :

= 18/24 + 4/24 - 15/24

= (18 + 4 - 15)/24

= 7/24

Cross Multiplication

In adding and subtracting unlike fractions, if the denominators are co-prime or relatively prime, we have to apply this method.

For example, let us consider the addition of two fractions given below.

1/8 + 1/3

In the above two fractions, denominators are 8 and 3.

For 8 and 3, there is no common divisor other than 1.

So 8 and 3 are co-prime.

We can do cross multiplication to add or subtract this kind of fractions as shown below.

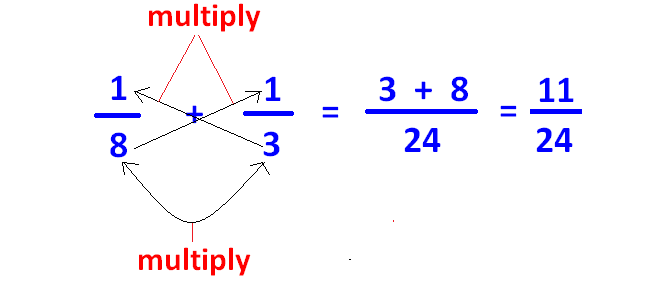
Example 7 :

Add 1/2 and 1/3.

Solution :

The given fractions are unlike fractions (having different denominators).

For the denominators 2 and 3, there is no common divisor other than 1.

So, 2 and 3 are co-prime or relatively prime.

We can do cross multiplication to add the given fractions.

= 1/2 + 1/3

= (2 + 3)/(2 x 3)

= 5/6

Example 8 :

Subtract 3/10 from and 5/9.

Solution :

The given fractions are unlike fractions (having different denominators).

For the denominators 10 and 9, there is no common divisor other than 1.

So, 10 and 9 are co-prime or relatively prime.

We can do cross multiplication to add the given fractions.

= 5/9 - 3/10

= (50 - 27)/(9 x 10)

= 23/90

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.