ADD SUBTRACT AND MULTIPLY LINEAR EXPRESSIONS WORKSHEET

1. Add (6a + 3) and (4a - 2).

2. Add (5y + 8 + 3z) and (4y - 5).

3. Subtract (6a - 3b) from (-8a + 9b).

4. Subtract (2x + 3y - 5z) from (5x - 4y - 5z).

5. Multiply (3x - 7) and (7x - 3).

6. Multiply (3a - 2b) and (2a + 3b).

7. Multiply (p + q + r) and (p + q - r).

8. Simplify : 2(3p + 5q) - 5(p + 4q) + 2(5p - 1).

9. Simplify : (3x + 5y + 3) - 2(x + 4y - 1) + 2(3x + 5).

10. Simplify : (3x + 5y + 3) - 2(x + 4y - 1) + 2(3x + 5).

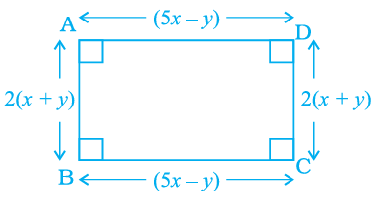
11. Find the perimeter of the figure given below:

12. A wire is (7x – 3) metres long. A length of (3x – 4) metres is cut for use. Now, answer the following questions:

(a) How much wire is left?

(b) If this left out wire is used for making an equilateral triangle. What is the length of each side of the triangle so formed?

13. After x is increased by 22, then halved, and finally decreased by 4, the result is 12. What is the value of x?

14. If 30 more than 25 percent of x is 20 less than 75 percent of x, what is the value of x?

15. Write the following statements in the form of algebraic expressions and write whether it is monomial, binomial or trinomial.

(a) x is multiplied by itself and then added to the product of x and y.

(b) Three times of p and two times of q are multiplied and then subtracted from r.

1. Answer :

= (6a + 3) + (4a - 2)

 = 6a + 3 + 4a - 2

= 10a + 1

2. Answer :

= (5y + 8 + 3z) + (4y - 5)

 = 5y + 8 + 3z + 4y - 5

= 9y + 3z + 3

3. Answer :

= (-8a + 9b) - (6a - 3b)

 = -8a + 9b - 6a + 3b

= -14a + 12b

4. Answer :

= (5x - 4y - 5z) - (2x + 3y - 5z)

= 5x - 4y - 5z - 2x - 3y + 5z

= 3x - 7y

5. Answer :

= (3x - 7)(7x - 3)

= 21x² - 9x - 49x + 21

= 21x² - 58x + 21

6. Answer :

= (3a - 2b)(2a + 3b)

= 6a² + 9ab - 4ab - 6b²

= 6a² + 9ab - 4ab - 6b²

= 6a² + 5ab - 6b²

7. Answer :

= (p + q + r)(p + q - r)

Let x = p + q.

= (x + r)(x - r)

Using Algebraic Identity a² - b² = (a + b)(a - b),

= x² - r²

Substitute x = p + q.

= (p + q)² - r²

Using Algebraic Identity (a + b)² = a² + 2ab + b².

= p² + 2pq + q² - r²

8. Answer :

= 2(3p + 5q) - 5(p + 4q) + 2(5p - 1)

= 2(3p) + 2(5q) - 5(p) - 5(4q) + 2(5p) + 2(-1)

= 6p + 10q - 5p - 20q + 10p - 2

= 11p - 10q - 2

9. Answer :

= (3x + 5y + 3) - 2(x + 4y - 1) + 2(3x + 5)

= 3x + 5y + 3 - 2(x) - 2(4y) - 2(-1) + 2(3x) + 2(5)

= 3x + 5y + 3 - 2x - 8y + 2 + 6x + 10

= x - 3y + 15

10. Answer :

= (2y + 3)(y - 4) - 5y(3y - 1)

= 2y(y) + 2y(-4) + 3(y) + 3(-4) - 5y(3y) - 5y(-1)

= 2y² - 8y + 3y - 12 - 15y² + 5y

= -13y² - 12

11. Answer :

length = 5x - y

Width = 2(x + y)

Perimeter of rectangle = 2(length + width)

= 2(5x - y + 2(x + y))

= 2(5x - y + 2x + 2y)

= 2(7x + y)

= 14x + 2y

12. Answer :

Length = (7x – 3) metres

length of wire to be cut = (3x – 4) metres

(a) Quantity of wire left = 7x - 3 - (3x - 4)

= 7x - 3 - 3x + 4

= 7x - 3x - 3 + 4

= 4x + 1

(b) Perimeter of equilateral triangle = 4x + 1

3(side length) = 4x + 1

side length = (1/3)(4x + 1)

13. Answer :

x is increased by 22, then x + 22

then halved = (x + 22)/2

Finally decreased by 4, then (1/2)(x + 22) - 4

Result = 12

(1/2)(x + 22) - 4 = 12

(1/2) (x + 22) = 12 + 4

(1/2) (x + 22) = 16

x + 22 = 16(2)

x + 22 = 32

x = 32 - 22

x = 10

So, the value of x is 10.

14. Answer :

25% of x + 30 = 75% of x - 20

0.25x + 30 = 0.75x - 20

0.25 x - 0.75 x = -20 - 30

-0.50x = -50

x = 50/0.50

x = 100

So, the value of x is 100.

15. Answer :

a) x(x) + xy

x² + xy

b)  r - 3p (2q)

= r - 6pq

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.