SHSAT PRACTICE TEST QUESTIONS IN MATH

Question 1 :

One-third the product of two numbers is 24. One-half the product of these same two numbers is

(A) 72 (B) 54 (C) 48 (D) 36 (E) 12

Solution :

Let "x" and "y" be the two numbers.

Product of two numbers = xy

(1/3) of xy = 24

xy = 24(3)

xy = 72

Multiply 1/2 on both sides, we get

(1/2) xy = (1/2) 72

(1/2) xy = 36

Hence the required answer is 36.

Question 2 :

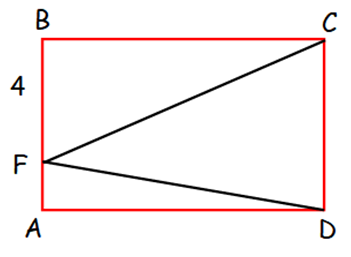
The area of rectangle ABCD is 72. Point F is on AB such that BF = 4. What is the sum of the areas of triangles CBF and DAF?

(A) 18 (B) 24 (C) 36 (D) 42

(E) Cannot be determined from the given information

Solution :

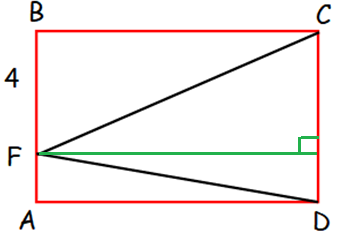
By subtracting area of triangle FDC from area of rectangle ABCD, we get the required area.

Required area = Area of ABCD - Area of triangle FDC

= 72 - (1/2) base ⋅ height

= 72 - (1/2) (CD ⋅ AD)

CD = Width of rectangle, AD = Length of rectangle

= 72 - (1/2) (Area of rectangle)

= 72 - (1/2) (72)

= 72 - 36

= 36

Hence the required area is 36.

Question 3 :

Ms. Brady has 28 students in her class. The ratio of boys to girls in the class is 2 to 5. How many new boys must be added to the class to make the ratio of boys to girls 1:2?

(A) 1 (B) 2 (C) 4 (D) 12 (E) 32

Solution :

Number of students in the class = 28

Number of boys = (2/(2+5)) ⋅ 28

= (2/7) ⋅ 28

= 2(4)

= 8

Number of girls = 5/(2+5) ⋅ 28

= (5/7) ⋅ 28

= 5(4)

= 20

(8 + y) : (20 + y) = 1 : 2

(8 + y) / (20 + y) = 1/2

2(8 + y) = 1 (20 + y)

16 + 2y = 20

2y = 20 - 16

2y = 4

y = 2

Hence the number of students to be added is 2.

Question 4 :

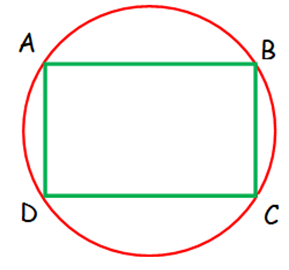
The vertices of rectangle ABCD all lie on the same circle as shown. The circumference of the circle is 64π. What is the length of AC?

(A) 8 (B) 16 (C) 32 (D) 64 (E) 128

Solution :

AC is the diagonal of the rectangle as well diameter of the circle.

Circumference of circle = 64π

2πr = 64π

2 ⋅ r = 64

r = (64/2)

r = 32

Diameter of the circle (AC) = 2(32) = 64.

Question 5 :

Ten cards are numbered 10, 11, 12,. . . . , 19, one number per card. Brain removes three cards whose numbers are primes, and puts the remaining cards in a hat. If one card is then drawn at random from the hat, what is the probability that its number is a prime?

(A) 1/10 (B) 1/9 (C) 1/5 (D) 2/5 (E) None of these

Solution :

Sample space = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19}

Prime numbers between 10 and 19

= {11, 13, 17}

There are only three prime numbers between 10 and 19. After removing these prime number, there is no chance of getting prime number.

So, the probability of getting prime number after removing these prime numbers is 0.

Question 6 :

In the figure, all line segments meet at right angles. What is the area enclosed by the figure?

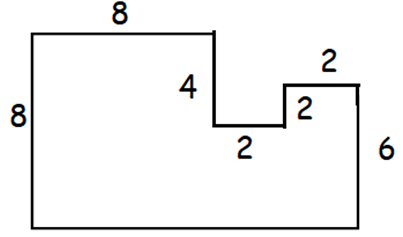
(A) 84 (B) 72 (C) 70 (D) 68 (E) 64

Solution :

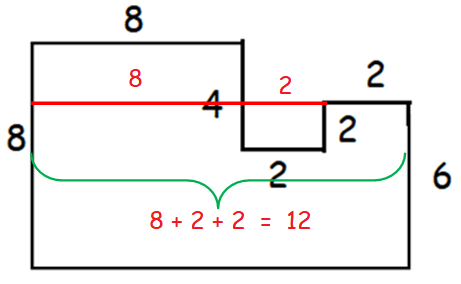
From the picture given above, length of the rectangle is 12 and width of the rectangle is 8.

Area of the rectangle = length ⋅ Width

= 12 (8)

= 96

Required area

= 96 - (area of square of side length 2 + area of rectangle with length and width are 4 and 2 respectively)

= 96 - [2² + 4(2)]

= 96 - [4 + 8]

= 96 - 12

= 84

Question 7 :

The perimeter of a square is four times the circumference of a circle with radius of 1 m. What is the area of the square ?

(A) 4π² (B) 2π² (C) π² (D) π

(E) cannot be determined.

Solution :

Perimeter of square = 4 Circumference of circle

Radius of circle = 1 m

4a = 4(2π r)

4a = 8π (1)

a = 8π/4 ==> 2π

Area of square = a²

= (2π)²

= 4π²

Question 8 :

Assume that the notation ┴ (q, r, s, t) means “Multiply q and r, then add the product to s and divide by t”. What is the value of ┴(2, 6, 4, 8) + ┴ (4, 7, 2, 6)?

(A) 7.0 (B) 7.5 (C) 8.0 (D) 8.5 (E) 9.0

Solution :

┴(2, 6, 4, 8)

By comparing it with ┴ (q, r, s, t), we get

q = 2, r = 6, s = 4 and t = 8

In general :

┴ (q, r, s, t) = (qr + s)/t

┴(2, 6, 4, 8)

= (2(6) + 4)/8

= 16/8

= 2 ---(1)

┴ (4, 7, 2, 6)

= (4(7) + 2)/6

= (28 + 2)/6

= 30/6

= 5 ---(2)

(1) + (2)

= 2 + 5

= 7.0

Hence the answer is 7.0

Question 9 :

When the sum of a list of integers is divided by the mean of the integers, the result is x. What does x represent?

(A) the sum of the integers

(B) half the sum of the integers

(D) the number of integers in the list

(E) half the number of integers in the list

Solution :

Mean = Sum of all numbers / Number of terms

Here, we divide sum of a list of integers by mean. So we get Number of integers.

Question 10 :

A piece of paper is used to make a cylinder (without a top and bottom) that is 8 inches long and has a radius of 1.5 inches. Assuming no part of the paper overlaps, what is the area of the piece of paper?

(A) 12 sq. in. (B) 24 sq. in. (C) 6 sq. in.

(D) 6 sq. in. (E) 24 sq. in.

Solution :

Curved surface area of cylinder = 2πrh

Height = 8 inches, Radius = 1.5 inches

= 2 π (8) (1.5)

= 24 π square inches.