SHSAT PRACTICE QUESTIONS WITH ANSWERS

Question 1 :

For how many values of x is the function is not equal to 1 ?

f(x)  =  (x - 3)/(x - 3)

(A)  0    (B)  1    (C)  2    (D)  3    (E) infinitely many

Solution :

Since the numerator and denominator are same, we always get the value 1 for f(x).

So, the answer is infinitely many.

Question 2 :

If today is Monday, what day will it be in 49² from now ?

(A)  Tuesday  (B)  Wednesday  (C)  Thursday 

(D)  Monday  (E)  Sunday

Solution :

First let us find the value of 49²

49²  =  49 ⋅ 49  =  2401

To find the day after 2401 days from now, we have to divide 2401 by 7 to get the remainder.

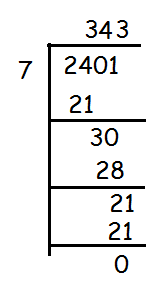
We get 0 as remainder. According to day arithmetic, 0 stands for Sunday.

Hence the day after 2401 from now is Sunday.

Question 3 :

If f(x)  =  x³, then what times is f(4) than f(2) ?

(A)  2  (B)  3  (C)  4  (D)  8  (E)  10

Solution :

f(4)  =  64

f(4)  =  8 (8)

f(4)  =  8 [f(2)]

Hence f(4) is 8 times of f(2).

Question 4 :

In the figure, point B is on line segment AC and point D is on line segment AE. The value of x + y is.

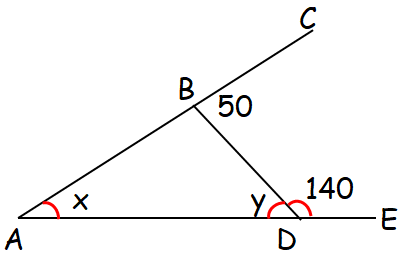
(A)  50  (B)  70  (C)  75  (D)  90  (E)  140

Solution :

In triangle ABD,

<BAD + <ADB + <DBA  =  180  ----(1)

<ABD + DBC  =  180

<ABD + 50  =  180

<ABD  =  130

By applying the value of <ABD in (1), we get

x + y + 130  =  180

x + y  =  50

Question 5 :

How many prime numbers are between 4 and 16 inclusive ?

(A)  2  (B)  3  (C)  4  (D)  5  (E)  6

Solution :

4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16

Prime numbers are 5, 7, 11, 13

Hence there are 4 prime numbers between 4 and 16.

Question 6 :

How many perfect squares are between 9 and 25 exclusive ?

(A)  0  (B)  1  (C)  2  (D)  3  (E)  4

Solution :

9, 16, 25

Hence the number of perfect square between 9 and 25 is 1.

Question 7 :

On the number line, point R (not shown) is to the right of Q and PQ is 1/5 of PR. What is the coordinate of R ?

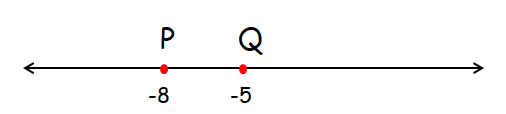
(A)  7      (B)  15     (C)  23     (D) 25      (E) 40

Solution :

Given that :

PQ  =  (1/5) of PR

PQ  =  (1/5) ⋅ PR

5 PQ  =  PR

Distance between P and Q  =  -8 - (-5)

  =  -8 + 5

  =  -3 (that is 3 units)

So, the distance between P and R must be 15 units. To get the distance 15 units, let us choose the first option and test whether it satisfies or not.

PR  =  - 8 - 7  =  - 15 (that is 15 units)

Hence the coordinate of R is 7.

Question 8 :

If (x/y)  =  x², then what is (x/y) - (x/y)² ?

(A)  x²  (B)  x² y  (C)  x⁴  (D) x²(1-x²)  (E) x²(1+x²)

Solution :

(x/y) - (x/y)²  =  x² - (x²)²

  =  x² - x⁴

  =  x² (1 - x²)

Question 9 :

In scale drawing, 1 millimeter represents 150 meters. How many square millimeters on the drawing represent 1 square meter ?

(A)  1/150  (B)  1/22500  (C)  150/22500 

(D)  120  (E) 22500

Solution :

If 1 mm represents 150 m, then 1 sq.mm represents 225 00 sq.m.

1 sq.m  =  (1/22500) sq.mm

Question 10 :

A rectangle is drawn on the coordinate plane. If the coordinates of one corner of the rectangle is (0, -5) and the coordinates of the opposite corner is (7, 3), then what is the area of the rectangle ?

(A)  -56  (B)  -21  (C)  21  (D)  56  (E)  105

Solution :

To solve this problem, first let us draw a rectangle in a coordinate plane with given conditions.

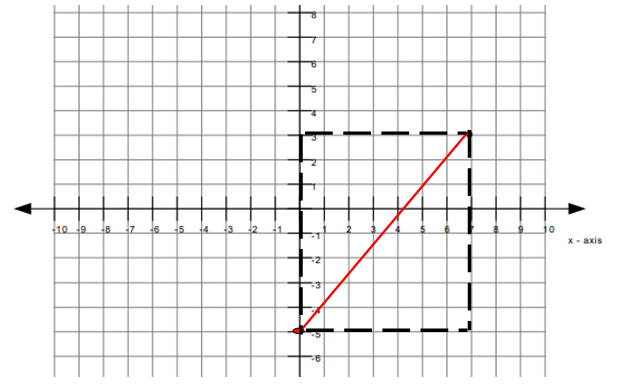
From the given picture, the length of rectangle is 7 units and width of the rectangle is 8 units.

Area of rectangle  =  length (width) 

  =  7(8)

  =  56 square inches.

MORE SHSAT QUESTION PAPERS

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.