SHSAT PRACTICE QUESTIONS AND ANSWERS IN MATH

Question 11 :

Express 6.925 x 10⁵ in standard form.

Solution : 

  =  6.925 x 10⁵

  =  6.925 x 100000

  =  692500

Question 12 :

On the number line above, X is located at -10, Y is at -2, and Z is at 8.  M (not shown) is the midpoint of XY, and N (not shown) is the  midpoint of YZ.  What is the midpoint of MN?

Solution :

Y is located at -2 and X is located at -10.

Numbers between X and Y are

-2, -3, -4, -5, -6, -7, -8, -9, -10

The midpoint of these two numbers is -6.

So, M is located at -6.

Numbers between Y and Z are

-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8

So, N is located at 3.

Now, let us write the numbers between -6 and 3.

-6, -5, -4, -3, -2, -1, 0, 1, 2, 3

-1.5 is the midpoint of MN.

Question 13 :

If 0 < y < 1, which of the following statements must be true?

(A)  y² > y³  (B)  y > 0.5y  (C)  y > y³ 

(D)  All of the above  (E)  None of the above

Solution :

Let x = 0.5

By applying the value of y in option A, we get

0.25 > 0.125  True

By applying the value of y in option B, we get

0.5 > 0.5 (0.5)

0.5 > 0.25  True

By applying the value of y in option C, we get

0.5 > (0.5)³

0.5 > 0.125  True

Hence all of the above is true.

Question 14 :

The area of the square ABCD is 4 times larger than the area of square WXYZ.  If the area of square WXYZ is 9, what is the difference between the length of a side of square ABCD and the length of a side of square WXYZ?

Solution :

Area of the square ABCD  =  4 Area of the square WXYZ

Area of the square WXYZ  =  9

a²  =  9

a  =  3

Side length of square WXYZ  =  3

Area of the square ABCD  =  4(9)  =  36

s²  =  36

s  =  6

Difference between side length of ABCD and WXYZ

  =  6 - 3 

  =  3

Question 15 :

Triangle GHI is similar to Triangle JKL.

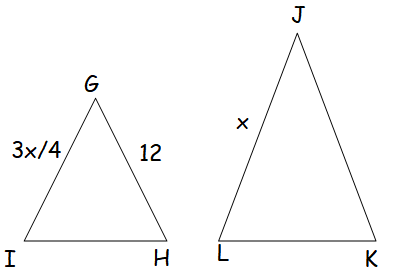
What is the length of side JK?

Solution :

Since the above triangles are similar, the length of the sides are in the same ratio.

GI/JL  =  GH/JK  =  IH/ LK

(3x/4)/x  =  12/JK  =  IH/LK

3/4  =  12/JK

JK  =  12(4)/3

 JK  =  16

Question 16 :

Wesley and two of his friends are driving cross country nonstop and have agreed to take turns driving in 7-hours shifts.  Each person will drive for one shift, and take two shifts off to rest.  If Wesley’s first shift starts at 6:00 a.m., at what time will Wesley complete his third shift?

Solution :

Hence the required answer is 7 : 00 AM.

Question 17 :

What is the difference between the largest and lowest integer in the sequence of consecutive odd integers whose sum is 15 ?

Solution :

Let us select three numbers 3, 5 and 7.

3 + 5 + 7  =  15

Difference between largest and lowest integer 

=  7 - 3 

=  4

Hence the answer is 4.

Question 18 :

The half life of a substance is the time it takes for a substance to decrease to half its initial amount. John has a pile of goo that decreases in amount at a constant rate. If John initially had 100 pounds of goo, and ten days later, he only had 25 pounds of goo, what is the half of the goo ?

Solution :

In 10 days, the goo decreased by 2 half lives. So each life is 5 days.

Question 19 :

What is the value of (9⁴ - 8⁴)/(9² + 8²) ?

Solution :

(9⁴ - 8⁴)/(9² + 8²)  =  [(9²)² - (8²)²] / (9² + 8²)

  =  [(9² + 8²) (9² - 8²)] / (9² + 8²)

  =  9² - 8²

  =  81 - 64 

  =  17

Hence the answer is 17.

Question 20 :

Jackie fills a jug with water continuously. It takes her 2 minutes to fill up 50% of the empty space in the jug with water. After every 2 minutes, she puts a penny into a jar to celebrate. How many pennies will she have in the jar at the instant the jug has less than 30% empty space left ?

Solution :

Now Jackie starts to fill the jug. At the first round, he fills 50% of empty space in the jug in 2 minutes and drop a penny.

Now the jug contains 50% of empty space. If he fills half of the 50% of empty space at that instant, the quantity of water will become 75%. Hence the condition will not satisfy, by filling water in the second round.

So, there is only 1 penny in the jar at the instant the jug has lesser than  30% of empty space.

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.