SHSAT MATH SAMPLE TEST QUESTIONS AND ANSWERS

Question 11 :

If N = √(36 + 49), then N is

Solution :

N = √(36 + 49)

N = √85

The square root of 81 is 9.

But root 85 is greater than 81, the number between 9 and 10.

Question 12 :

Susan is 5 years older than Phen is now.  In N years, Susan will be twice as old as Phen is now.  If Susan is now 22 years old, what is the value of N?

Solution :

Let "x" be Phen's age

x + 5 be Susan's age

x + 5 + N  =  2x  ---(1)

Now Susan's age =  22 years 

x + 5  =  22

x  =  22 - 5  =  17

By applying the value of x in (1)

17 + 5 + N  =  2(17)

22 + N  =  34

N  =  34 - 22

N  =  12

Question 13 :

The number of integer values of n for which 1 ≤ √n ≤ 3 is

Solution :

 1 ≤ √n ≤ 3

√1  =  1

√2  = 1.41....

√3  = 1.73

√4  =  2

√5  =  2....

√9  =  3

Hence 9 is number of integer values of n.

Question 14 :

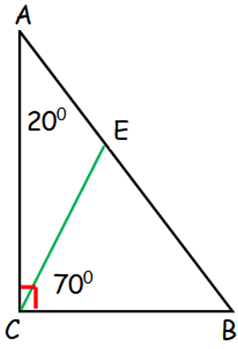
In right triangle ABC, angle ACB is 90°.  The  number of degrees in angle BEC is

Solution :

In triangle ACB :

<ACB + <CBA + <BAC  =  180

90 + <CBA + 20  =  180

<CBA  =  180 - 110  =  70

Now consider the triangle CEB,

<CEB + <CBE + <BCE  =  180

  <CEB + 70 + 70  =  180

<CEB  =  180 - 140

<CEB  =  40

Question 15 :

If it is now 12:00 noon, what time was it 40 hours ago?

Solution :

40 + 12  =  52

By dividing 52 by 12, we get the quotient 4 and remainder as 4.

Now, we have to move the clock 4 hours back word from 12 : 00 noon. So we get 8 : 00 AM.

Question 16 :

The mean of all the odd integers between 6 and 24 is

Solution :

First let us list out the odd integers between 6 and 24.

7, 9, 11, 13, 15, 17, 19, 21, 23

So, there are 9 odd numbers lies between 6 and 24.

Mean  =  (7 + 9 + 11 + 13 + 15 + 17 + 21 + 23)/9

  =  135/9

  =  15

Question 17 :

Let x be an element of the set {0.2, 1.2, 2.2, 3.2, 4.2}.  For how many values of x is 10x/3 an integer?

Solution :

Let f(x)  =  10x/3 

Hence for 2 values of x, we get integer.

Question 18 :

George has just enough money to buy 3 chocolate bars and 2 ice cream cones.  For the same amount money, he could buy exactly 9 chocolate bars.  For the same amount of money, how many ice cream cones could George buy?

Solution :

Let "x" and "y" be the cost of one chocolate bar and one ice cream cone.

3x + 2y  =  f(x)  ---(1)

Cost of 9 chocolate bars  =  9x  =  f(x)  ----(2)

(1)  =  (2)

3x + 2y  =  9x

  2y  =  9x - 3x

  2y  =  6x

   y  =  3x  ==> x  =  y/3

By applying y = 3x in (1), we get

3(y/3) + 2y  =  f(x)

y + 2y  =  f(x)

f(x)  =  3y

Hence, we can buy 3 ice cream cone for the same amount.

Question 19 :

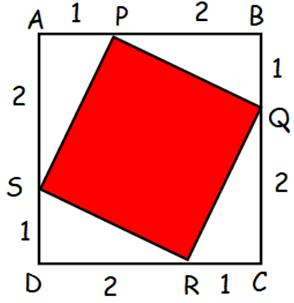
ABCD and PQRS  are squares, as shown.  The area of PQRS is

Solution :

To find the side length pf RS, we have to use Pythagorean theorem.

In triangle DSR,

SR²  =  SD² + DR²

SR²  =  1² + 2²  =  5

SR  =  √5

Area of the square PQRS  =  a²

  =  (√5)²  =  5

Question 20 :

If x = 10 and y = 8, what is the value of y (3x – 2y)?

Solution :

  =  y(3x – 2y)

x = 10, y = 8

  =  8(3(10) – 2(8))

  =  8 (30 - 16)

  =  8 (14)

  =  112

More Practice Test Papers

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.