SHSAT MATH PRACTICE TEST

Question 11 :

In a diagram, each small box is a square whose side is 3. What is the area of the shaded figure ?

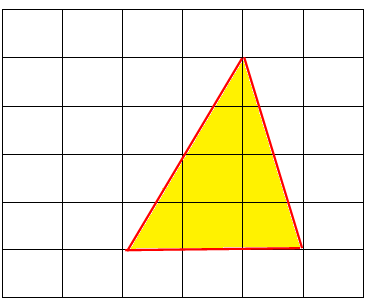
(A)  108  (B)  54  (C)  36  (D)  18  (E)  6

Solution : 

Base of the triangle  =  3 units => 3 x 3 ==> 9

height  =  4 units ==> 4 x 3 ==> 12

Area of triangle  =  (1/2) ⋅ base ⋅ height 

  =  (1/2) ⋅ 9 ⋅ 12

  =  54 square units

Question 12 :

When expressed in scientific notation, the number

1,230,000,000 is 1.23 x 10^B.

The value of B is 

(A)  2  (B)  7  (C)  8  (D)  9  (E)  10

Solution :

Scientific notation of the given number

1,230,000,000  =  1.23 x 10⁹

Since we move the decimal 9 digits to the left side, we use positive sign.

Hence the value of B is 9.

Question 13 :

In a diagram, lines m and n are parallel. What is the value of x ?

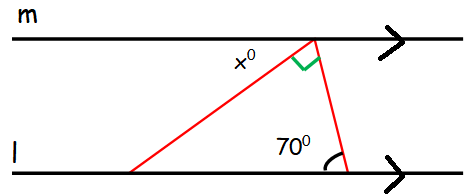
(A)  20  (B)  40  (C)  45  (D)  60  (E)  70

Solution :

Here l and m are parallel lines.

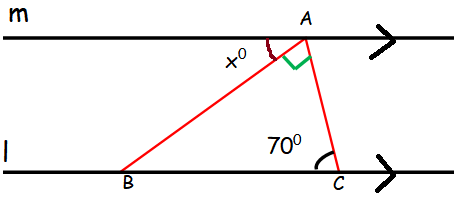
In a triangle, sum of angles  =  180

<ABC + <BAC + <BCA  =  180

<ABC + 90 + 70  =  180

<ABC + 160  =  180

<ABC  =  180 - 160

<ABC  =  20  =  x (alternate interior angles)

Hence the value of x is 20.

Question 14 :

If p  =  √(2 + √10), Q  =  √(10 + √2) and R = √(5 + √5)

(A)  P < Q < R   (B)  P < R < Q  (C)  Q < R < P 

(D)  R < Q < P  (E)  P  =  Q

Solution :

Approximate value of P :

The approximate value of √10 is 3.....

By adding 3.... and 2, we get 5......... By taking √5......, we get 2.......

Approximate value of Q :

The approximate value of √2 is 1.....

By adding 1.... and 10, we get 11......... By taking √11......, we get 3.......

Approximate value of R :

The approximate value of √5 is 2......

By adding 2.... and 5, we get 7......... By taking √7......, we get 2.......

P  =  √5......, Q  =  √11...... and R  =  √7......

Hence the answer is P < R < Q.

Question 15 :

The sides of a triangle all have integer lengths. Two side have lengths 7 and 10. If the largest and smallest possible perimeters for the triangle are L and S, the value of L + S.

(A)  is 20  (B)  is 51  (C) is 52 (D)  is 54 

(E)  cannot be determined from the information given

Solution :

Any side of a triangle has to be greater than the difference of the other 2, and less than the sum of the other 2

c > 10 - 7

c > 3

c < 10 + 7

c < 17

The smallest integer value is 4, and the largest is 16.

S  =  7 + 10 + 4  =  21

L  =  7 + 10 + 16  =  33

L + S  =  54

Question 16 :

Evaluate (1/2) + (1/3) - (1/4)  = 

(A)  1/20  (B)  7/12  (C)  3/4  (D)  1  (E)  13/12

Solution :

L.C.M (2, 3 and 4)  =  12

To convert the denominator of first fraction as 12, we have to multiply both numerator and denominator by 6.

(1/2) ⋅ (6/6)  =  6/12  ----(1)

The second fraction by 4

(1/3) ⋅ (4/4)  =  4/12  ----(2)

The third fraction by 3

(1/4) ⋅ (3/3)  =  3/12  ----(3)

(1) + (2) - (3)

  =  (6/12) + (4/12) - (3/12)

  =  (6 + 4 - 3)/12

  =  7/12

Question 17 :

 In the diagram, AC  =  BD  =  17 and BC  =  3. The length of segment AD is 

(A)  20  (B)  24  (C)  28  (D)  31  (E)  34

Solution :

To find the length of AD, we have to add the lengths of AB, BC and CD.

AD  =  AB + BC + CD  

  =  14 + 3 + 14

  =  31

Hence the answer is 31.

Question 18 :

What is the value of |x - y| + |y - x| if x = -3 and y = -7 ?

(A)  -14  (B)  -6  (C)  0  (D)  8  (E)  20

Solution :

|x - y| + |y - x|  =  4 + 4  =  8

Hence the answer is 8.

Question 19 :

The sum 2¹⁰ + 1¹⁰ + (1/2)¹⁰ + (1/3)¹⁰ + (1/4)¹⁰ is closest to

(A)  21  (B)  32  (C)  513   (D)  1025  (E)  2000

Solution :

2¹⁰  =  1024

2¹⁰  =  1

Other than the above two, the values of other terms will be too small.

Hence the sum is closest to 1025.

Question 20 :

4³ + 4³ + 4³ + 4³  =  

(A)  4⁴  (B)  4⁹  (C)  4¹²  (D)  16³  (E)  16¹²

Solution :

4³ + 4³ + 4³ + 4³  =  4(4³)

  =  4^{(1 + 3)}

  =  4⁴

More Practice Test Papers

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.