SHSAT MATH PRACTICE QUESTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 11 :
The probability of picking a piece of dark chocolate out of a bowl of candy is 5/6. Which of the following could NOT be the number of pieces of candy in the bowl?
(A) 6 (B) 11 (C) 24 (D) 30 (E) 60
Solution :
Probability of getting dark chocolate = 5/6
In the given options, we may change the denominators as 6, 24, 30 and 60. But we could not change the denominator as 11.
Hence the required answer is 11.
Question 12 :
Two pyramids are glued together base to base. The area of each base is 25 square inches, and the height of one of the pyramids is 3 in.The other pyramid is twice as high. What is the total volume of the combined figure?
(A) 25 cu. in (B) 50 cu. in (C) 75 cu. in
(D) 100 cu. in (E) 125 cu. in
Solution :
Area of the base of pyramid = 25 square inches
Height of one pyramid = 3 inches
Height of other pyramid = 2(3) = 6
Total height new pyramid = 3 + 6 = 9
Volume of pyramid = (l ⋅ w ⋅ h)/3
= (25 ⋅ 9)/3
= 25 (3)
= 75 cubic inches
Question 13 :
If a = 2b3/c, what happens to the value of a when both b and c are doubled ?
(A) a is not changed (B) a is halved
(C) a is doubled (D) a is tripled
(E) a is multiplied by 4.
Solution :
If b = 2b and c = 2c
a = 2(2b)3/(2c)
= 2(8b3/2c)
= 8b3/c
= 4(2b)3/c
Hence a is multiplied by 4 is the answer.
Question 14 :
In a class poll, 24 students chose pizza as their favorite food, 15 students chose hamburgers, and 1 student chose neither. What fraction of the students polled chose pizza?
(A) 3/5 (B) 4/5 (C) ¼ (D) 3/8 (E) 5/8
Solution :
Number of students who choose pizza = 24
Number of students who choose hamburgers = 15
Number of students who choose neither = 1
Total number of students = 24 + 15 + 1 = 40
Fraction of students who choose pizza = (24/40)
= 3/5
Question 15 :
What is the value of √(16 + 9) – (√16 + √9) ?
(A) -2 (B) 0 (C) 2 (D) 4 (E) 6
Solution :
= √(16 + 9) – (√16 + √9)
= √25 – (4 + 3)
= 5 – (4 + 3)
= 5 - 7
= -2
Hence the answer is -2.
Question 16 :
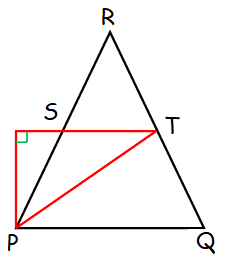
In the above figure, triangle PQR is equilateral, S is located at the midpoint of PR , and T is located at the midpoint of QR. What is the degree measurement of angle PST?
(A) 120 (B) 125 (C) 135 (D) 150 (E) 180
Solution :
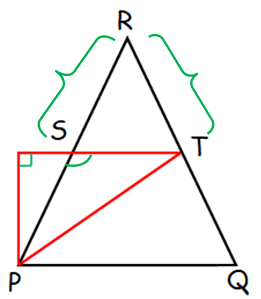
RS = RT
(Since S and T are the midpoints of the side PR and RQ)
Equal side makes an equal angle.Since RPQ is equilateral triangle, <PRQ = 60°
In triangle RST,
<RST + <STR + <SRT = 180
<RST + <STR + 60 = 180
<RST + <STR = 120
2<RST = 120
<RST = 60
<RST + <PST = 180
60 + <PST = 180
<PST = 120
Hence the answer is 120 degree.
Question 17 :
Pete's living expenses
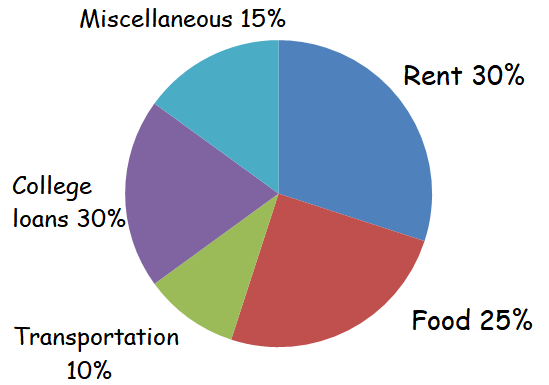
The graph above shows the distribution of Pete’s $1,200 living expenses. Pete has two roommates and splits the cost of rent with them equally, so the amount he pays for rent is only part of the total rent for the apartment in which he lives. What is the total rent for Pete’s apartment ?
(A) $360 (B) $720 (C) $1,080
(D) $1,200 (E) $1,333
Solution :
Pete's share = 30% of 1200
= 360
Since he has two room mates, Pete's share
= 360 + 360 + 360
= $1080
Question 18 :
At noon, Bradley began steadily increasing the speed of his car by 2 miles per hour every minute. At 12:15 p.m., he realized he was going 15 miles per hour over the speed limit. If his speed at noon was 40 miles per hour, what was the speed limit. If his speed at noon was 40 miles per hour, what was the speed limit at 12:15 p.m.?
(A) 50 (B) 55 (C) 60 (D) 65 (E) 70
Solution :
At noon means 12 : 00 PM,
The speed at 12 : 00 PM is 40 miles per hour.
From 12 : 00 to 12 : 15 PM, we have 15 minutes.
Speed within 15 minutes = 2 (15) = 30
But he realizes, he was going 15 miles per hour over the speed limit.
= 40 + 30 - 15
= 70-15
= 55 miles per hour.
Question 19 :
(2 + 3) x (4 – 2)2
If the parenthesis were removed from the above expression, what would be the change in the value of the expression?
(A) There will be no change in value
(B) a decrease of 4 (C) a decrease of 10
(D) a decrease of 18 (E) a decrease of 186
Solution :
Value before removing parenthesis :
= (2 + 3) x (4 – 2)2
= 5 x 22
= 5 x 4
= 20
Value after removing parenthesis :
= 2 + 3 x 4 – 22
= 2 + 12 -4
= 14 - 4
= 10
Hence the answer is a decrease of 10.
Question 20 :
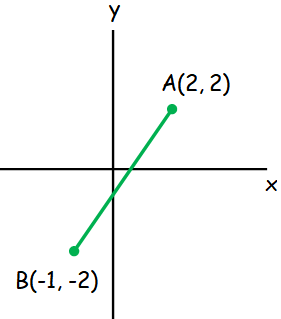
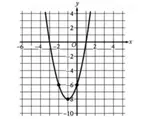
Point C (not shown) is on the midpoint of AB. What is the y-coordinate of point c?
(A) -1.0 (B) -0.5 (C) 0 (D) 0.5 (E) 1.0
Solution :
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (-1 + 2)/2, (-2 + 2)/2
= 1/2, 0/2
= (0.5, 0)
y-co ordinate is 0.
You might like these
SHSAT math practice test - Paper 1
SHSAT math practice test - Paper 2
SHSAT math practice test - Paper 3
SHSAT math practice test - Paper 4
SHSAT math practice test - Paper 5
SHSAT math practice test - Paper 6
SHSAT math practice test - Paper 7
SHSAT math practice test - Paper 8
SHSAT math practice test - Paper 9
SHSAT math practice test - Paper 10
SHSAT math practice test - Paper 11
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Solving Problems on Percentage
Mar 03, 26 04:54 AM
Solving Problems on Percentage -
Digital SAT Math Problems and Solutions (Part - 35)
Mar 03, 26 04:39 AM
Digital SAT Math Problems and Solutions (Part - 35) -
Digital SAT Math Problems and Solutions (Part - 37)
Mar 03, 26 04:03 AM
Digital SAT Math Problems and Solutions (Part - 37)