SHSAT MATH PRACTICE QUESTIONS AND ANSWERS

Question 1 :

Phone Company A charges 50 + 3x dollars for an international phone plan, where x is the number of minutes spent talking.  Phone Company B charges 60 + 2x dollars for an international phone plan, where x is the number of minutes spent talking.  What is the price at which both companies charges the same amount?

(A)  $10  (B)  $20  (C)  $30  (D)  $80  (E)  $110

Answer :

Charge of company A  =  50 + 3x

Charge of company B  =  60 + 2x

50 + 3x  =  60 + 2x

3x - 2x  =  60 - 50

x  =  10 (Number of minutes)

Charge of company A  =  50 + 3(10)

=  50 + 30

=  $80

Hence the price is $80.

Question 2:

William, Xing Mei, Yuki, and Zack run a race.  In how many different ways can they finish?

(A)  4  (B)  16  (C)  24  (D)  32  (E)  64

Answer :

There are 4! ways to finish the race.

4!  =  4 ⋅ 3 ⋅ 2 ⋅ 1

  =  24

Hence they may finish the race in 24 ways.

Question 3 :

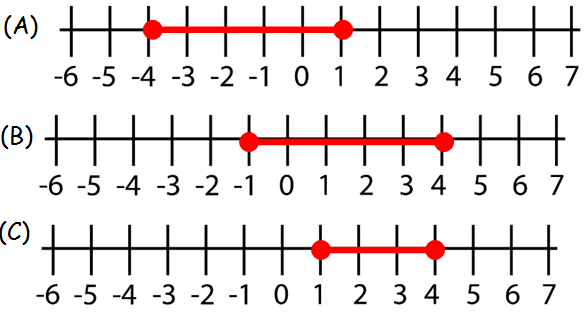
What is the solution set for -1 ≤ -2f + 1 ≤ 9?

Answer :

-1 ≤ -2f + 1 ≤ 9

  =  -1 - 1 ≤ -2f ≤ 9 - 1

  =  -2 ≤ -2f  ≤ 8

  =   -2 ≤ -2f  ≤ 8 

Divide by (-2)

  =   1 ≥ f ≥ -4 

=  -4 ≤ f ≤ 1 

Hence option A is correct.

Question 4 :

On a blueprint of a school 1/4 inch represents 24 feet.  If the cafeteria is 60 feet long, what is its length, in inches, on the  blue print ?

(A)  3/8  (B)  5/8  (C)  3/4  (D)  1 ¼  (E) 2 ½

Answer :

24 feet  =  1/4 inch

Divide by 24 on both sides

1 feet =  (1/4) / (24) inch

1 feet  =  1/96 inch

60 feet  =  60(1/96) inch

  =  (60/96) inch

  =  (5/8) inch

Question 5 :

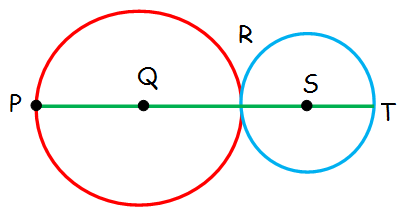
In the above figure, the two circles are tangent at point R.  The length of PR = 8.  The area of the circle with center Q is 4 times larger than the area of the circle with center S.What is the length of QS ?

(A)  6  (B)  8  (C)  10  (D)  12  (E)  16

Answer :

Length of PR  =  8

PQ = QR  =  4  (radius)

Area of the circle with center Q  =  4 (Area of circle with center S)

Area of circle with center Q  =  πr²

 =  π(4²)  =  16π

16π  =  4 π(RS)²

4  =  (RS)²

RS  =  2

QS  =  QR + RS

QS  =  4 + 2

QS  =  6

Question 6 :

Lenny's average score after 3 tests is 88. What score on the 4^th test would bring Lenny's average upto exactly 90?

(A)  92  (B)  93  (C)  94  (D)  95  (E)  96

Answer :

Sum of 3 test scores  =  3 (88)  =  264

Sum of 4 test scores  =  4(90)  =  360

4^th test score  =  360 - 264

  =  96

Hence 4^th test score is 96.

Question 7 :

Darius ran 1/6 as many times around the track as Ezekiel.  Darius ran around the track 2 ⅔ times.  How many times did Ezekiel run around the track?

(A)  8  (B)  10  (C)  12  (D)  14  (E)  16

Answer :

Let "x" be the number of times that Ezekiel around the track, then 

Darius ran around the track  =  (1/6)x  =  x/6

Now, Darius ran around the track  =  2 ⅔ times

  =  8/3

We need to show 8/3 in terms of 1/6.

For that, let us multiply the numerator and denominator by 2.

So, we get 

  =  (8/3) ⋅ (2/2)

  =  16/6

  =  (1/6) ⋅ 16

Hence Ezekiel run around the track 16 times.

Question 8 :

A decagon has 10 sides and 10 angles.  What is the average number in degrees in each interior angle of a decagon ?

(A)  140  (B)  144  (C)  1,296  (D)  1,400  (E)  1,440

Answer :

All sides are of same length (congruent) and all interior angles are same (congruent).

To find the measure of the angles, we know that the sum of all the angles is 1440 degrees

Average  =  1440/10  =  144

Hence the interior angle is 144 degree.

Question 9 :

The table below show a relationship between x and y values.

(A)  y = 0.5x + 2  (B)  y = x + 1  (C)  y = 2x + 1 

(D)  y = 3x – 2  (E)  y = 4x – 1

Answer :

If x  =  0, y  =  1

If x  =  2, y  =  5

In the given options, option C satisfies the above conditions.

Hence option C is correct.

Alternative Method :

Equation of the line :

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

(y - 1)/(5 - 1)  =  (x - 0)/(2 - 0)

(y - 1)/4  =  x/2

2(y - 1)  =  4x

y - 1  =  2x

y  =  2x + 1

Question 10 :

|x - 3 ⋅ 5| = 6 + y, |9 – y + 6| = 21

In the equations above, y < 0. What is the value of x?

Answer :

|x - 3 ⋅ 5| = 6 + y

|x - 15| = 6 + y

x - 15  =  6 + y   (or)   -x + 15  = 6 + y

x - y  =  6 + 15    (or)  -x - y  =  6 - 15

x - y  =  21------(1)  (or)  -x - y  =  -9-----(2)

(1) + (2)

-2y  =  12

y  =  -6 < 0

x  =  21 + y ==>  x  =  21 - 6  =  15

Hence the value of x is 15.

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.