FREE ACT MATH PROBLEMS

Question 1 :

In a cricket team of 11 players, the average age of 4 players is 17, the average of 3 players is 18 and the average of 2 players is 19. The average age of the whole team is 18. One of the players is aged 22. Find the age of the last player.

Solution :

Average of 11 players  =  18 years

Total age of 11 players  =  18 x 11

=  198

Average of 4 players  =  17 years

Total age of 4 players  =  4 x 17

=  68

Average of 3 players  =  18 years

Total age of 3 players  =  3 x 18

=  54

Average of 2 players  =  19 years

Total age of 2 players  =  2 x 19

=  38

Age of another player  =  22 years

Total age of 10 players  =  68 + 54 + 38 + 22

=  182 years

Age of last player  =  198 - 182

=  16 years

Therefore the required age  =  16 years.

Question 2 :

A fruit merchant bought 1200 mangoes for $1000.300 fruits went bad. He sold fruits at $18 per dozen, and the bad fruits at $9 per dozen. Find his total gain or loss per cent in the transaction.

Solution :

Cost price of the mangoes  =  $1000

Number of good fruits  =  900

Number of dozens of good fruit  =  900/12

=  75 dozens

Selling price of 1 dozen  =  $18

Selling price of 75 dozens  =  75 x 18

=  1350

Number of bad fruits  =  300

Number of dozens of bad fruits  =  300/12

=  25 

Selling price of 1 dozen bad fruit  =  $9

Selling price of 25 dozens of bad fruits  =  9 x 25

=  $225

Total selling price  =  1350 + 225

=  $1575

Profit  =  Selling price - Cost price 

=  1575 - 1000

=  $575

Profit percent  =  (profit amount/cost price)   x 100

=  (575/1000) x 100

=  57.5 %

Question 3 :

Walking at a constant rate of 8 kilometers per hour, Juan can cross a bridge in 6 minutes. What is the length of the bridge in meters? (1 kilometer = 1000 meters)

A. 480    B. 600    C. 720    D. 750    E. 800

Solution :

Speed = 8 kilometer per hour

1 kilometer = 1000 meters

Converting speed into minutes

= 8 x (1000/60)

= 400/3

Time taken by Juan = 6 minutes

Length of bridge :

Time = distance / speed

Distance = time x speed

= 6 x (400/3)

= 2(400)

= 800 meters

Question 4 :

In order to qualify for the year-end tennis tournament, Sam must win at least 60 percent of his matches this year. To date, Sam has won 14 of his 18 matches. Of Sam’s 13 matches remaining in the year, what is the least number that he must win in order to qualify for the year-end tournament?

A. 4     B. 5     C. 6    D. 7      E. 8

Solution :

Total number of matches she plays in the year = 18 + 13

= 31 matches

In this she should win 60% of the matches 

= 60% of 31

= (60/100) x 31

= 18.6

Number of matches she should win is 18.

So far, she won 14 matches. Then the number of matches yet to be played = 18 - 14

= 4 matches

So, option A is correct.

Question 5 :

Five years from now, Tatiana will be two years older than Frederico is now. If Frederico is currently thirteen, how old is Tatiana now?

A. 8     B. 10     C. 13    D. 15    E. 18

Solution :

Let x be Frederico's present age.

Five years from now, age of Tatiana = x + 2

Applying x = 13, then x + 2 will be 15.

So, option D is correct.

Question 6 :

In the Antares Corporation, 3/7 of the managers are female. If there are 42 female managers, how many managers in total are there?

A. 18      B. 24     C. 60     D. 66      E. 98

Solution :

Let x be the total number of managers.

3/7 of x = 42

3x/7 = 42

x = 42 (7/3)

x = 98

So, the total number of managers are 98.

Question 7 :

A company has 40 executives and 120 customer service representatives. If these are the only employees, what percentage of the employees are executives?

A. 20%    B. 25%     C. 33%     D. 40%     E. 80%

Solution :

Number if executives = 40

Number of customer service representatives = 120

Total number of employess = 40 + 120

= 160

percentage of executives = (40/160) x 100%

= (1/4) x 100%

= 25%

Question 8 :

If R = 10b² and b = 5, then R =

A. 25    B. 50     C. 100     D. 250    E. 500

Solution :

R = 10b²

Applying b = 5

R = 10(5)²

R = 10(25)

R = 250

So, option D is correct.

Question 9 :

A prism with dimensions given in centimeters is shown below. If the volume of a prism is the area of a triangular base times the length of a rectangular base, what is the volume of this prism, in cubic cm?

A. 30     B. 40     C. 50    D. 60    E. 120

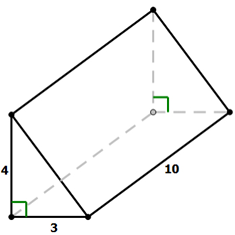
Solution :

Volume of prism = base area x height

base area = 1/2 x base x height

= 1/2 x 3 x 4

= 6 cm²

height of prism = 10 cm

volume of prism = 6 x 10

= 60 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.