9th GRADE SHSAT SAMPLE QUESTIONS

Question 1 :

How many multiples of 3 between 1 and 22 are even?

(A)  7  (B)  5  (C)  3  (D)  1  (E)  None

Solution :

Multiples of 3 lies between 1 and 22.

3, 6 9, 12, 15, 18, 21

Hence there 7 numbers lies between 1 and 22. 

Question 2 :

2x(3y) =

(A)  12xy  (B)  6xy  (C)  5xy  (D)  6x + 6y  (E)  5x + 5y

Solution :

2x(3y) =  6xy

Question 3 :

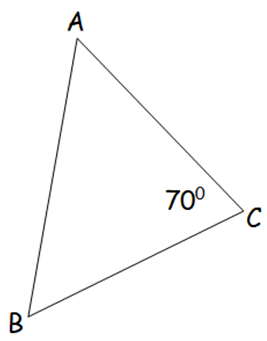
In triangle ABC, AB=AC and the measure of angle C is 70°.  What is the  measure of angle A, in degrees?

(A)  40  (B)  55  (C)  60  (D)  70  (E)  90

Solution :

Since AB and AC are equal, they form equal angles.

<B  =  70

In a triangle, sum of interior angles will be 180

<A + <B + <C  =  180

<A + 70 + 70  =  180

<A  =  180 - 140

<A  =  40

Hence the measure of angle A is 40°.

Question 4 :

√36 x √9 + √16  =

(A)  √340  (B)  22  (C)  30  (D)  42  (E)  150

Solution :

  =  √36 x √9 + √16

  =  √(6 ⋅ 6) ⋅ √(3 ⋅ 3) + √(4 ⋅ 4)

=  6 ⋅ 3 + 4

=  18 + 4

=  22

Hence the answer is 22.

Question 5 :

At 9 A.M. it was 12 degrees below zero.  By noon the temperature had dropped 7 degrees.  Over the next two hours, the temperature rose  5 degrees.  What was the temperature at 2 P.M.?

(A)   0°  (B)  10° below zero  (C)  14° below zero 

(D)  24° below zero  (E)  none of these

Solution :

At 9 A.M the temperature was 12 degrees below zero.

At 12 P.M, the temperature has dropped 7 degree

So, the temperature was  =  -12 - 7  =  -19

After two hours from 12 P.M, the temperature rose 5 degrees

At 2 PM, the new temperature will be  =  -19 + 5

  =  -14 degree

Hence 14° below zero is the required answer.

Question 6 :

Bob’s age is now 3 times Tom’s age.  Twelve years from now, Tom will be 15 years old.  How many years old is Bob now?

(A)  3  (B)  5  (C)  9  (D)  27  (E)  45

Solution :

Let "x" be Tom's age.

After 12 years, Tom's age will be 15.

x + 12  =  15

x  =  15-12  =  3

Tom's present age  =  3

Bob's present age  =  3 times Tom’s present age

  =  3 (3)

  =  9

Hence the required age is 9 years.

Question 7 :

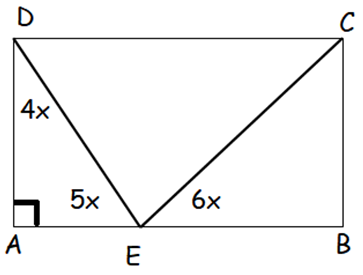
In rectangle ABCD, point E is on side AB.  What is the measure of angle DEC ?

(A)  10°  (B)  48°  (C)  60°  (D)  70°  (E)  90°

Solution :

First let us consider the triangle ADE,

<A  =  90

4x + 5x + 90  =  180 

9x + 90  =  180

9x  =  90

x  =  10

Let <DEC  =  y 

5x + 6x + y  =  180

11 x + y  =  180

11(10) + y  =  180

110 + y  =  180

y  =  180 - 110  =  70

Hence the required angle is 70 degree.

Question 8 :

If 1 < 4n < 50, and n is a positive Integer, what is the largest possible value for n ?

(A)  199  (B)  49  (C)  13  (D)  12.5  (E)  12

Solution :

1 < 4n < 50

Divide the entire equation by 4. 

1/4 < n < 50/4

Integer means, a number should not have decimal point.

1/4  =  0.25 and 50/4  =  12.5

Integers lies between these decimals are 

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Hence there are 12 integers.

Question 9 :

Which of the following is equal to (8x-8)/2 ?

(A)  8x – 4  (B)  4x – 4  (C)  4x – 8  (D)  4x  (E)  4

Solution :

  =  (8x - 8)/2

  =  2(4x - 4)/2

  =  4x - 4

Question 10 :

If 7x – 14 = 14 – 7x, then x =

(A)  -4  (B)  -2  (C)  0  (D)  2  (E)  4

Solution :

7x – 14 = 14 – 7x

Add 7x on both sides

7x + 7x - 14  =  14

Add 14 on both sides

14x  =  14 + 14

14x  =  28

x  =  28/14

x  =  2

Hence the value of x is 2.

More Practice Test Papers

SHSAT math practice test - Paper 1

SHSAT math practice test - Paper 2

SHSAT math practice test - Paper 3

SHSAT math practice test - Paper 4

SHSAT math practice test - Paper 5

SHSAT math practice test - Paper 6

SHSAT math practice test - Paper 7

SHSAT math practice test - Paper 8

SHSAT math practice test - Paper 9

SHSAT math practice test - Paper 10

SHSAT math practice test - Paper 11

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.