ZEROS OF A POLYNOMIAL

Let P(x) represent a polynomial. To find the zeros of the polynomial, we have to set P(x) equal to zero and solve for x.

Zeros of a Linear Polynomial

Find the zeros of each of the following polynomials.

Example 1 :

p(x) = 2x + 3

Solution :

p(x) = 0

2x + 3 = 0

Subtract 3 from both sides.

2x = -3

Divide both sides by 2.

x = -³⁄₂

Example 2 :

p(x)  =  4x - 1 

Solution :

p(x) = 0

4x - 1 = 0

Add 1 to both sides.

4x = 1

Divide both sides by 4.

x = -¼

Zeros of a Quadratic Polynomial

Example 3 :

p(x) = x² + 17x + 60

Solution :

p(x) = 0

x² + 17x + 60 = 0

The above quadratic equation can be solved by factoring.

In the quadratic equation, 'x² + 17x + 60 = 0', the coefficient of x² is 1 and the constant term is '+60'. We have to get two factors for '+60' such that the product of the two factors is '+60' and the sum of the two factors is  '+17', which is the coeffient of x.

Such two factors of '+60' are '+12' and '+5'.

x² + 17x + 60 = 0

x² + 12x + 5x + 60 = 0

x(x + 12) + 5(x + 12) = 0

(x + 12)(x + 5) = 0

x + 12 = 0  or  x + 5 = 0

x = -12  or  x = -5

The zeros of the given quadratic polynomial are -12 and -5.

Example 4 :

p(x) = x² - 4x + 1

Solution :

p(x) = 0

x² - 4x + 1 = 0

In the quadratic equation, 'x² - 4x + 1 = 0', the coefficient of x² is 1 and the constant term is '+1'. We have to get two factors for '+1' such that the product of the two factors is '+1' and the sum of the two factors is  '-4', which is the coeffient of x.

But, we can not get such two factors for '+1'.

So, the quadratic equation 'x² - 4x + 1 = 0' can not be solved by factoring.

We can solve this kind of quadratic equations using quadratic formula.

Comparing 'ax² + bx + c = 0' and 'x² - 4x + 1 = 0', we get

a = 1, b = -4 and c = 1

Quadratic Formula :

Substitute a = 1, b = -4 and c = 1.

x = 2 ± √3

x = 2 - √3 or 2 + √3

The zeros of the given quadratic polynomial are 2 - √3 and 2 + √3.

Zeros of a Cubic Polynomial

Example 5 :

p(x) = x³ - 5x² - 4x + 20

Solution :

p(x) = x³ - 5x² - 4x + 20

x³ - 5x² - 4x + 20 = 0

The above cubic equation can be solved by factoring. The expression on the left side of the equation can be factored by grouping.

(x³ - 5x²) + (-4x + 20) = 0

x²(x - 5) - 4(x - 5) = 0

(x² - 4)(x - 5) = 0

The zeros of the given cubic polynomial are -2, 2 and 5.

Example 6 :

p(x) = 4x³ - 7x + 3

Solution :

p(x) = 4x³ - 7x + 3

4x³ - 7x + 3 = 0

The above cubic equation can not be solved by factoring. So, we can use synthetic division to solve the above cubic equation.

By trial and error, we can check 1 or -1 or 2 or -2..... can be the zeros of the given cubic polynomial using synthetic division.

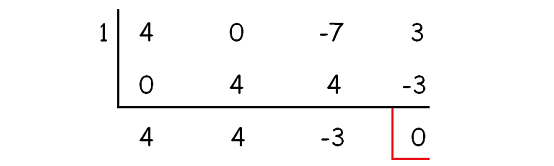
When we divide the given cubic polynomial by (x - 1), the remainder is zero.

So, x = 1 is one of the zeros of the given cubic polynomial.

The quotient is (4x² + 4x - 3).

Set the quotient equal to zero and solve for x.

4x² + 4x - 3 = 0

Multiply the coefficent of x², 4 by the contant term -3. The product is -12. Now, we have to get two fators for -12 such that product is equal to -12 and the sum is equal to +4.

Such two factors are -2 and +6.

4x² - 2x + 6x - 3 = 0

2x(2x - 1) + 3(2x - 1) = 0

(2x - 1)(2x + 3) = 0

2x - 1 = 0  or  2x + 3 = 0

x = ½  or  x = -³⁄₂

The zeros of the given cubic polynomial are -³⁄₂, ½ and 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.